Номер 11. ЕГЭ по информатике

Теория

Про кодирование информации

Информатика — это наука о работе с информацией. Прежде всего нам интересно, как эта работа происходит внутри компьютера. Поэтому возникает очень важная задача. Необхоимо сохранить информацию, с которой мы работаем. Это может быть текст, картинки, звукозаписи, прочие формы. Информация вокруг нас существует в разных видах. Однако проблема в том, что в компьютере, устройстве универсальном, который мы используем повсеместно для работы с информацией, данные хранятся лишь в одном единственном формате — в виде двоичного кода, в виде набора нулей и единиц. Компьютер устроен так, что он способен воспринимать исключительно двоичную форму представления данных. Всё, что хранится в вашем компьютере, будь то фотографии, текстовые сообщения, музыка, видеоролики — всё это закодировано последовательностью нулей и единиц.

Вопрос для нас стоит следующий: как информация становится набором нулей и единиц?

Любая информация проходит через два этапа:

Дискретизация
Кодирование

Начнём с первого шага — дискретизации. Важно отметить, что вся информация глобально делится на две категории: аналоговую и цифровую.

Примечание Джобса: здесь Алексей имеет в виду формы передачи или представления информации. Сама информация не может обладать физическими характеристиками. Поэтому далее под «аналоговая информация» и «дискретная информация» будет подразумеваться именно форма представления информации, а не её свойства.

Аналоговая информация обладает важным свойством — непрерывностью. Её невозможно разделить на отдельные части, она представляет собой постоянный, плавный поток. Вся доступная человеку информация вокруг нас является аналоговой: всё, что мы видим, слышим, ощущаем органами чувств, относится к этой группе. Однако компьютер неспособен эффективно обрабатывать такую информацию, поскольку оперирует исключительно числами — нулями и единицами. Поэтому информация должна быть разделена на небольшие фрагменты.

Цифровая информация представлена в виде множества мелких элементов («кирпичиков»). Из таких кирпичиков, например, формируется целое изображение. Картина на экране вашего монитора состоит из пикселей — мельчайших светящихся точек. Если взять сильную увеличительную линзу и рассмотреть экран внимательно, вы заметите, что изображение составлено именно из них. Звук также воспринимается нами непрерывно, однако в компьютере записанный звук представлен множеством отдельных моментов, создающих иллюзию звуковой волны. По факту это совокупность отдельных точек, которые настолько близки друг другу, что человек не замечает разницы. То же самое справедливо и для трёхмерной графики: поверхности объектов представлены совокупностью полигонов и вершин, а текст — комбинацией буквенных знаков.

Таким образом, вся информация дробится на элементарные составляющие, которые удобно представить в виде чисел. Именно поэтому для компьютерной обработки информация должна быть представлена в цифровом виде, поскольку лишь тогда возможна дальнейшая обработка компьютером. После того как информация представлена в таком удобном формате, начинается второй этап — непосредственное преобразование фрагментов в двоичные коды.

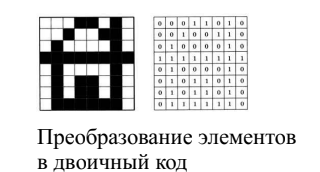
Каждый элемент, представляющий фрагмент информации, имеет заранее известное фиксированное число возможных значений. Рассмотрим конкретный пример: пусть это будет пиксель экрана. У каждого пикселя есть заданный диапазон возможных цветов, пусть это палитра. Каждое конкретное значение цвета представлено уникальной последовательностью нулей и единиц согласно принятой схеме кодировки. Такая схема определяет правила перевода элемента информации в бинарный код и обратно. Таким образом, каждая единица информации преобразуется в свою уникальную цепочку нулей и единиц, которую компьютер легко сохраняет и воспроизводит впоследствии.

Возвращаясь к примеру с изображением: зная цвет каждой точки, мы можем восстановить изображение на экране. Для этого компьютер читает двоичный код и интерпретирует его соответствующим образом. Например, исходя из последовательности нулей и единиц, он окрашивает пиксель в нужный оттенок. Точно так же восстанавливается и текст: компьютеру известно соответствие конкретного символа конкретной комбинации нулей и единиц.

Теперь разберёмся подробнее с пикселем. Пиксель — это минимальная составляющая изображения, представленная точкой. Цвет каждого пикселя определяется количеством красного, зелёного и синего компонентов, выражаемых двоичными кодами. Каждый пиксель отображён на экране посредством светодиодов, управляемых двоичной системой компьютера.

Итак, повторим ещё раз основные моменты теории: вся информация, поступающая в компьютер, сначала подвергается процессу деления на элементарные части, после чего каждая часть переводится в уникальный двоичный код. Это правило лежит в основе всей информационной системы компьютера. Весь объём хранящейся в нём информации представлен последовательностью нулей и единиц.

Важно понимать, что есть два подхода к процессу преобразования информации. Два метода кодирования.

Первый называется равномерным. Это наиболее распространённый метод. То есть двоичный код каждого «кирпичика» всегда представлен последовательностью фиксированной длины. Это удобно, поскольку данные легко записать и считать: одинаковый размер позволяет быстро обрабатывать информацию.

Второй подход — неравномерный, когда длина фрагментов переменная: некоторые фрагменты короче, другие длиннее. Такой способ уменьшает общий объём информации, экономит место. Однако тут возникают свои особенности, трудности и ограничения.

Определение количества бит для кодирования

Представьте себе, что вы находитесь на месте первопроходцев компьютерного дела, размышляющих над задачей сохранения текста внутри компьютера. Эти новаторы задумались: каким образом записать текстовую информацию? Одним из первых предложенных ими способов стала идея кодировочной таблицы. Именно такую таблицу, называющуюся ASCII, вы можете увидеть перед собой. Она представляет собой первую систему кодирования.

Суть идеи заключалась в следующем: был составлен перечень возможных знаков, используемых в тексте. Сюда вошли разнообразные вспомогательные символы, применяемые для разметки текста, а также простенькие знаки вроде чисел и букв латинского алфавита, больших и маленьких. Затем эти символы были выстроены последовательно, каждому присвоив собственный бинарный код фиксированной длины — ровно семь бит. Каждый символ обозначался уникальной последовательностью из семи нулей и единиц.

Таким образом, разработчики создали полный список возможных символов, встречающихся в тексте, закрепив за каждым из них уникальный идентификатор равной длины. Так возникла система кодирования ASCII, применявшаяся долгие годы. Важно отметить, что данная кодировка является равномерной, поскольку длина кода постоянна и равна семи битам.

Но возникает вопрос: достаточно ли такого набора символов для современных нужд? Очевидно, сегодняшняя ситуация сильно отличается от той, что существовала раньше. Сегодняшние тексты включают огромное разнообразие символов: помимо привычных латинских букв, присутствуют кириллические, восточные иероглифы, даже смайлы. Поэтому теперь используется значительно расширенная версия кодировки — Unicode, включающая сотни тысяч разных знаков, включая древние и современные пиктограммы. Для записи столь большого числа символов семи битов уже недостаточно, и теперь применяются длинные коды длиной до 16 бит.

И отсюда вытекает простое правило: чем больше уникальных символов мы желаем зафиксировать, тем длиннее должны быть соответствующие коды.

Если добавить новый язык — она расширится, скажем, что Unicode — каждый год эта кодировочная таблица ежегодно увеличивается. Каждый год специальный консорциум Unicode добавляет новые символы в кодировку. Это не только эмодзи, например, сюда входят также разнообразные языки, служебные символы, обозначения, значки и прочее. Здесь важно отметить, что при упоминании 16-битного символа стоит осознавать, что количество возможных значений настолько велико, что свободных мест хватит ещё надолго. Поэтому данная кодировка столь обширна и вмещает всё необходимое. Они изначально выделили большое число битов на каждый символ, увеличивая пространство постепенно. Изначально история была следующей: некоторое время использовалось 8 бит, как, например, кодировка ASCII и подобные ей.

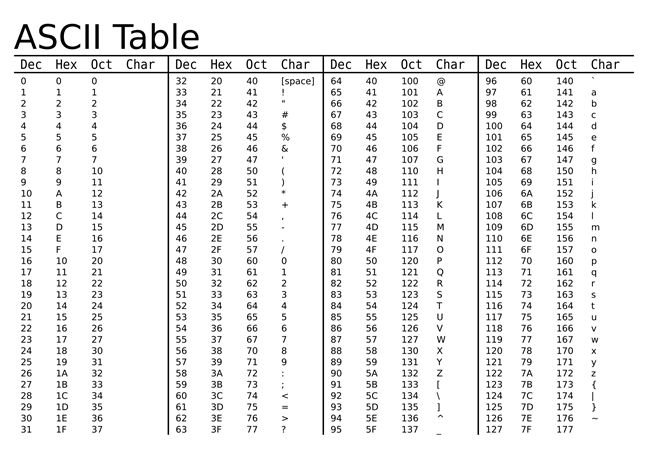
Затем произошёл переход к 16-битной версии. Почему именно такой резкий скачок, расскажу немного позднее — в нём есть определённый смысл. Итак, 16-битная версия обладает огромной ёмкостью, позволяя разместить огромное количество символов, причём место ещё остаётся. Так выглядит работа текстовых кодировок. Есть таблица, посмотрим её хотя бы на секунду. Например, современную таблицу Unicode, выводящую символы этой кодировки. Мы видим здесь начало, совпадающее с ASCII-кодировкой, после которого идут всевозможные значки — огромная коллекция самых разных знаков. Присутствует кириллица, арабские, сирийские, самаритянские, бенгальские символы… Здесь собрано практически всё возможное. Даже некоторые знаки просто не отображаются — отсутствует соответствующий значок. Представьте себе, сколько всего здесь содержится. Эти группы символов наглядно демонстрируют их разнообразие. Итак, 16 бит означают длину строки в 16 двоичных цифр.

Примечание Джобса: у Unicode есть несколько реализаций кодировочных таблиц. Например, UTF-8 и UTF-16 имеют неравномерный код, UTF-32 – равномерный.

Теперь перейдём к следующему пункту нашего разговора: почему 16 бит — это много и сколько различных символов можно разместить в таком объёме? Как определить минимальное количество необходимых битов для записи некоторой информации?

Один бит представляет собой единицу измерения информации, равную одной единственной цифре. У этой цифры существует ровно два состояния: 0 и 1. То есть, один бит способен хранить данные, имеющие два противоположных значения типа «включён—выключён», «правильно—неправильно», «да—нет». Простую бинарную информацию вроде «есть—нет» можно выразить одним единственным битом.

Однако очевидно, что сложную информацию невозможно уместить в один бит. Если взять два бита, то количество возможных состояний увеличится до четырёх вариантов. Скажем, таким образом можно зашифровать цвета светофора: зелёный, жёлтый, красный плюс дополнительно состояние мигалки. Такая комбинация уже значительно богаче примитивного выбора «да—нет».

При трёх битах количество уникальных комбинаций возрастает до восьми. Далее, когда берём четыре бита, возникает уже 16 разных возможностей. Чем длиннее цепочка бит, тем больше возможных сочетаний.

Общая закономерность проста: длина последовательности из n бит позволяет представить 2^n уникальных значений. Например, если рассмотреть 16 бит, там будет 2^16, то есть 65 536 различных комбинаций.

Отсюда вопрос: зачем нужны другие системы счисления, скажем, шестнадцатеричная или восьмеричная? Мы обсудим это отдельно. Пока сосредоточимся на простой двоичной системе. Дело в том, что любое значение любого бита — это либо 0, либо 1. Когда вы имеете несколько последовательных бит, каждая позиция даёт два варианта. Чтобы найти общее количество возможных комбинаций, надо умножить число выборов каждой позиции. Получается 2*2*2…*2, то есть 2n.

Таким образом, один бит состоит из двух двоичных цифр, но фактически является одиночной цифрой, принимающей одно из двух возможных значений: ноль или единица.

Попробуем разобраться с задачей нахождения минимальной длины двоичного кода. Предположим, нам нужно закодировать обычные десятичные цифры — от нуля до девяти. Задача состоит в том, чтобы каждой цифре присвоить одинаково короткий двоичный код, причем самый экономичный вариант. Подумаем: возможно ли обойтись одним битом? Нет, конечно, ведь одному биту соответствуют всего две возможные комбинации — ноль и единица, а у нас целых десять цифр. Два бита дадут нам уже четыре комбинации — недостаточно, трех бит также не хватит. Минимальная длина, при которой удастся закодировать каждую цифру, начинается с четырех бит. Именно такой длины уникального кода хватает, чтобы однозначно обозначить любую цифру от нуля до девяти, причём еще останется резерв свободных кодовых комбинаций. Поэтому правильно говорить, что минимальное необходимое количество бит для представления десятичных цифр — четыре. Хотя теоретически можно было бы выделить больше места — скажем, десять или даже сотню бит, но наша цель — минимизировать затраты ресурсов. Рассмотрим теперь другой пример — английский алфавит, состоящий из двадцати шести букв. Теперь задача усложняется: четырех бит уже не хватит, потому что они позволяют создать максимум шестнадцать разных кодов, а нам нужно двадцать шесть. Зато пяти бит вполне достаточно: их ровно тридцать два комбинации, следовательно, каждая буква английского алфавита получит свою уникальную последовательность нулей и единиц. Для русского алфавита, который включает 33 буквы (с учетом буквы «ё»), потребуется уже большее количество бит.

И вот тут-то нас ждет сюрприз: всего пять бит, тридцать два возможных кода, а русских символов — аж тридцать три штуки. Не хватает ровно одного символа. Очень хочется избавиться от буквы «ё», но она значима, терять её никак нельзя. Значит, из-за одного символа, выходящего за удобное количество 32, придётся выделить шесть бит на каждый символ, потому что пятью битами все буквы русского алфавита не охватишь.

Теперь перейдём к латинице в верхнем и нижнем регистре. Верхний регистр — это прописные буквы, нижний — строчные. Получается отдельно коды для больших и отдельно для маленьких букв. Итак, имеем двадцать шесть больших и столько же маленьких букв. Всего получаем пятьдесят две разные комбинации. Но даже тут нам вполне хватит шести бит, ведь два в шестой степени даёт шестьдесят четыре возможных варианта.

Однако ситуация меняется, когда речь идёт о русской раскладке вместе с цифрами: сюда входят тридцать три больших, тридцать три малых буквы и еще десять цифр. Получаем семьдесят шесть уникальных знаков. А значит, шесть бит уже недостаточно, с помощью них можно закодировать только шестьдесят четыре комбинации. Следовательно, приходится добавлять еще один бит, доводя общую длину до семи. Такова простая логика выбора минимальной длины кодировки в битах методом подбора.

Задача № 1 (282)

При регистрации в компьютерной системе каждому пользователю выдаётся пароль, состоящий из 15 символов и содержащий только символы А, Б, В, Г, Д, Е. Каждый такой пароль в компьютерной программе записывается минимально возможным и одинаковым целым количеством байт, при этом используют посимвольное кодирование и все символы кодируются одинаковым и минимально возможным количеством бит. Определите, сколько байт необходимо для хранения 20 паролей.

Решение

Первое, с чего мы начнём, — создание собственной кодировки символов, используемых для записи пароля.. У нас всего 6 различных значений (А, Б, В, Г, Д, Е), которые нужно закодировать таким образом, чтобы каждый символ получил уникальный двоичный код одной и той же длины.

Один бит недостаточно, два бита также маловато, зато трёх бит уже хватает, чтобы присвоить уникальный код каждому символу. Таким образом, мы будем использовать трёхбитовую кодировку, где каждой букве соответствует собственный бинарный код (например, 000, 001, 010, 011, 100, 101).

Второй шаг — выясним, что именно записываем с её помощью. Записывать предстоит пароль фиксированной длины — 15 символов. Если представить простой пример пароля длиной пять символов («ABCDE»), то каждый символ представляется тремя битами. Получаем такую картину: G = 011, D = 100, E = 101. То есть вся строка ABCDE запишется последовательностью битов: 000 001 010 011 100 101. Сколько здесь цифр? Конечно, легко посчитать: 3 × 5 = 15 бит.

Для нашего случая имеем пароль длиной 15 символов, следовательно, 15 × 3 = 45 бит. Далее нам известно, что компьютер работает с информацией, представленной в байтах, а не в битах. Переводим полученные 45 бит в байты.

Поскольку 1 байт равен 8 битам, разделим 45 на 8, получим примерно 5,625 байта.

Но поскольку задана необходимость хранить целые байты и одинаковые для всех паролей, мы обязаны округлять вверх до ближайшего целого числа. Округляем результат и получаем ровно 6 байт на один пароль. Следовательно, для хранения двадцати паролей потребуется

20 × 6 = 120 байт.

Ответ: 120

Задача №2 (17)

При регистрации в компьютерной системе каждому пользователю выдаётся пароль, состоящий из 15 символов и содержащий только символы из 12-символьного набора: А, В, C, D, Е, F, G, H, K, L, M, N. В базе данных для хранения сведений о каждом пользователе отведено одинаковое и минимально возможное целое число байт. При этом используют посимвольное кодирование паролей, все символы кодируют одинаковым и минимально возможным количеством бит. Кроме собственно пароля, для каждого пользователя в системе хранятся дополнительные сведения, для чего выделено целое число байт; это число одно и то же для всех пользователей. Для хранения сведений о 20 пользователях потребовалось 400 байт. Сколько байт выделено для хранения дополнительных сведений об одном пользователе?

Решение

Для начала разберемся с принципом кодирования. Здесь используется алфавит из 12 уникальных символов. Соответственно, нам нужна такая схема кодирования, которая сможет однозначно представлять любые из этих 12 символов. Какое наименьшее количество бит потребуется для этого?
— 1 бит позволяет задать лишь две возможные комбинации (0 и 1);
— 2 бита обеспечивают четыре варианта (00, 01, 10, 11);
— 3 бита дадут 8 комбинаций;
— наконец, 4 бита позволяют записать целых 16 различных состояний (больше необходимого количества).
Следовательно, оптимальная кодировка будет иметь длину 4 бита на каждую букву пароля. Один символ теперь кодируется четырьмя битами.

Теперь подсчитаем общий объём пароля. Если пароль состоит из 15 символов, а каждый символ кодируется 4 битами, то пароль займет:
15 × 4 = 60 бит.
Переведём это в байты, поделив на 8:

608=7,5860=7,5Поскольку память выделяется целыми числами байт, округлим результат вверх: получаем ровно 8 байт на пароль.

Далее смотрим общую картину: есть 20 пользователей, которым совместно выделено 400 байт памяти. Определим средний расход на одного пользователя:40020 20400 = 20 байт.

Из этих 20 байт мы знаем, что 8 байт занято самим паролем. Остальное пространство зарезервировано под дополнительную информацию:
20 — 8 = 12 байт.
Итак, на дополнительные данные о пользователе отводится 12 байт.

Ответ: 12

Задача № 3 (5342)

При регистрации в компьютерной системе каждому объекту присваивается идентификатор, состоящий из 252 символов и содержащий только десятичные цифры и символы из 1700-символьного специального алфавита. В базе данных для хранения каждого идентификатора отведено одинаковое и минимально возможное целое число байт. При этом используется посимвольное кодирование идентификаторов, все символы кодируются одинаковым и минимально возможным количеством бит. Определите объём памяти (в Кбайт), необходимый для хранения 4096 идентификаторов. В ответе запишите только целое число – количество Кбайт.

Решение

Сначала рассмотрим систему кодирования. Какие элементы входят в неё? Во-первых, конечно, сами цифры от 0 до 9 — это десять вариантов. Плюс ещё имеем 1700 особых знаков. То есть всего необходимо закодировать 1710 разных элементов. Сколько бит потребуется?

Если взять 10 бит — получим 2¹⁰=1024, что недостаточно, ведь у нас больше возможных комбинаций. Попробуем увеличить до 11 бит — здесь получается 2¹¹=2048, что вполне достаточно. Следовательно, выберем именно 11 бит.

Далее считаем объём самого уникального номера. Нам надо длину строки (252 символа) умножить на выбранные 11 бит и поделить на восемь, чтобы получить число байт. Выходит около 346,5 байта. Округлим до ближайшего большего целого — это будет 347 байт.

Наконец, подсчитываем требуемый объём памяти для всех номеров вместе взятых. Перемножив 4096 номеров на 347 байт, найдем общий объём в байтах. Однако нужен ответ в килобайтах, следовательно, полученный результат делим на 1024 (так как 1 КБ равен 1024 байтам). Итоговый расчёт выглядит следующим образом:

4096⋅3471024 10244096⋅347 — получаем ровно 1388 килобайт.

Ответ: 1388

Задача № 4 (6733)

При регистрации в компьютерной системе каждому объекту присваивается идентификатор, состоящий из 213 символов и содержащий только десятичные цифры и символы из 1780-символьного специального алфавита. В базе данных для хранения каждого идентификатора отведено одинаковое и минимально возможное целое число байт. При этом
используется посимвольное кодирование идентификаторов, все символы кодируются одинаковым и минимально возможным количеством бит. Кроме собственно идентификатора, для каждого пользователя в системе хранятся дополнительные сведения, для чего выделено целое число байт, одинаковое для всех пользователей. Для хранения сведений о 297 пользователях потребовалось 130 680 байт. Сколько байт выделено для хранения дополнительных сведений об одном пользователе?

Решение

Кодировка состоит из десятичных цифр и специальных символов из данного алфавита. Таким образом, мы имеем 10 + 1780 = 1790 значений.

Чтобы закодировать такую кодировку, достаточно использовать минимальное количество битов, необходимое для представления всех возможных символов. Это 11 бит, поскольку 2¹¹ = 2048 > 1790.
Теперь рассмотрим длину идентификатора: 213 символов × 11 бит = 2343 бита.

Поскольку хранение осуществляется в байтах, разделим результат на 8:

2343882343≈ 292,875 → округляем до целого числа, получаем 293 байта.

Итак, теперь найдем общее потребление памяти одним пользователем:
Всего занято 130 680 байт для 297 пользователей. Тогда объем данных на одного пользователя составляет:

130,680297≈440297130,680≈440 байт

Вычтем размер идентификатора:
440 − 293 = 147.
Таким образом, для хранения дополнительных сведений об одном пользователе выделяется 147 байт.

Ответ: 147

Задача №5 (7468)

На предприятии каждой изготовленной детали присваивают серийный номер, содержащий десятичные цифры, 26 латинских букв (без учёта регистра) и символы из 8164-символьного специального алфавита. В базе данных для хранения каждого серийного номера отведено одинаковое и минимально возможное целое число байт. При этом используется посимвольное кодирование серийных номеров, все символы кодируются одинаковым и минимально возможным числом бит. Известно, что для хранения 835 серийных номеров отведено более 156 Кбайт памяти. Определите минимально возможную длину
серийного номера. В ответе запишите только целое число.

Решение

Сначала разберёмся с выбором подходящей кодировки для наших символов. У нас есть 10 цифр, 26 латинских букв и ещё дополнительно 8164 уникальных знака. Всего получаем:

10 + 26 + 8164 = 8200

возможных символов. Нам нужно выбрать такое количество бит, которое позволит хранить все возможные значения этих символов. Проверяем варианты:

Если взять 12 бит, то получится максимум 2¹²=4096, что недостаточно.
Если взять 13 бит, тогда доступно уже 2¹³=8192 комбинации — этого тоже мало.
Значит, придётся взять 14 бит (2¹⁴=16384), это число точно покрывает диапазон всех необходимых символов.

Теперь переходим ко второму этапу. Пусть N это размер номера. Каждый символ нашего серийного номера кодируется ровно 14-ю битами. Оценим объем занимаемой памяти для 835 номеров, зная, что общий объём превышает 156 Кб. Поскольку 1 Кб равен 1024 байтам, пересчитываем общую память в байты:

835*N > 156*1024

Отсюда следует, что N должен быть больше 191,31

Так как наш серийный номер хранится посимвольно, получим следующую формулу:
Общее количество символов × Размер одного символа > Необходимый объём памяти.
Пусть длина серийного номера равна x. Тогда:

x⋅148 8x⋅14 >191,31

Преобразуем выражение:

x > 191⋅81414191⋅8отсюда получаем:

x>109,14.

Минимальное подходящее целое число, большее 109,14 — это 110. Таким образом, минимальная возможная длина серийного номера составляет 110 символов.

Ответ: 110

Задание №6 (7926)

На предприятии каждой изготовленной детали присваивается серийный номер, состоящий из 377 символов. В базе данных для хранения каждого серийного номера отведено одинаковое и минимально возможное число байт. При этом используется посимвольное кодирование серийных номеров, все символы кодируются одинаковым и минимально возможным числом бит. Известно, что для хранения 23155 серийных номеров требуется более 5536 Кбайт памяти. Определите минимально возможную мощность алфавита, используемого для записи серийных номеров. В ответе запишите только целое число.

Решение

Мощность — это размер кодировки. Определим минимальный размер кодировки, который должен быть, чтобы выполнялось условие. Мы знаем, что 23155 номеров занимают больше указанного количества килобайт:

23155*N > 5536 * 1024 Байт

N > 244,82.

Итак, размер номера, чтобы выполнялось условие задачи, должен быть больше этой величины. Как посчитать размер номера в байтах?

Получится: берём длину строки — 377 символов, умножаем на размер символа i (сколько бит занимает символ). Делим на 8, переводим в байты, округляем обязательно в большую сторону. Эта округлённая величина должна быть больше 244,82.

377⋅i8>244,828377⋅i>244,82

Какой должна быть дробь, чтобы условие выполнялось без округления? Она должна быть просто больше 244.

Тогда отсюда можно прикинуть, каким должен быть размер символа:

244⋅8377377244⋅8

I >5,1

Получаем около 5,1 бита. Значит, минимальный размер символа — 6 бит.

Минимальный размер символа должен быть 6 бит. Почему именно 6? Если бы использовали 5 бит, то максимальный объём символов составил бы всего 2⁵ = 32 символа. Но поскольку задача требует большего размера, минимальное значение мощности алфавита — 33 символа. Таким образом, оптимальное решение, позволяющее соблюсти все условия, — это 33.

Ответ: 33

Задание № 7(7662)

В библиотеке каждой книге присваивают уникальный код, который может содержать десятичные цифры, 52 латинские буквы (с учётом регистра) и символы из 964-символьного специального алфавита. В базе данных для хранения каждого кода отведено одинаковое и минимально возможное целое число байт. Известно, что для хранения 3000 кодов отведено не более 1,5 Мбайта памяти. Определите максимально возможную длину кода. В ответе запишите только целое число.

Решение

Рассмотрим нашу систему кодирования подробнее. Она включает в себя десять цифр от нуля до девяти, 52 буквы латиницы с учётом различия регистров и ещё 964 особых символа. Если просуммируем эти значения, получим общее количество возможных знаков :

10 + 52 + 964 = 1026. Поскольку 1026 превышает показатель 2^10 (1024), для представления каждого символа потребуется минимум 11 бит.

Теперь перейдём непосредственно к подсчётам. Нам известно, что 3000 кодов занимают не более 1,5 мегабайт памяти. Так как 1 мегабайт равен 1024² байтам, получаем ограничение сверху равное:

3000*N<=1,5*1024 *1024

N <=524,288

Примем длину кода за х, тогда мы можем записать следующее выражение:

x⋅118<=5248x⋅11<=524

Отсюда:

24⋅811=1001124⋅8=100

X<=381,09

Приближённое значение показывает, что целочисленная максимальная длина равна 381. Именно столько символов может включать самый длинный уникальный библиотечный код согласно условиям задачи

Ответ: 381

Задание №8 (2066)

При регистрации в компьютерной системе каждому пользователю выдаётся пароль, состоящий из 7 символов. В качестве символов используют прописные и строчные буквы латинского алфавита (в нём 26 букв). В базе данных для хранения сведений о каждом пользователе отведено одинаковое и минимально возможное целое число байт. При этом используют посимвольное кодирование паролей, все символы кодируют одинаковым и минимально возможным количеством бит. Кроме собственно пароля, для каждого пользователя в системе хранятся дополнительные сведения, для чего выделено 12 байт на одного пользователя. В компьютерной системе выделено 2 Кб для хранения сведений о пользователях. О каком наибольшем количестве пользователей может быть сохранена информация в системе? В ответе запишите только целое число – количество пользователей.

Решение

Сначала рассчитываем необходимое количество бит для кодирования одного символа. Латинский алфавит содержит 26 заглавных и 26 строчных букв — итого 52 возможных варианта. Для кодирования такого количества значений потребуется минимум шесть бит (так как 2⁶ = 64, что больше необходимого числа).

Пароль состоит из семи символов, значит, для его кодирования понадобится:
7 × 6 = 42 бита.

Переведём полученное значение в байты:

428=5,5842=5,5 байт. Округлим вверх до ближайшего целого — получаем 6 байт.

Таким образом, пароль занимает 6 байт, а дополнительные данные — ещё 12 байт. Следовательно, общие затраты памяти на одного пользователя составляют:

6 + 12=18 байт.

Теперь определим максимальное количество пользователей, которое поместится в выделенные 2 КБ :

2⋅1024Байт18=100182⋅1024Байт=100

2*1024 Байт / 18 = 113,77

Округляя вниз, получаем итоговый результат: 113.

Ответ: 113

Задание №9(2045)

В некоторой стране автомобильный номер состоит из 8 символов. Первый символ – одна из 26 латинских букв, остальные семь – десятичные цифры. Пример номера – A1234567. Каждый символ кодируется минимально возможным количеством бит, а каждый номер – одинаковым и минимально возможным целым количеством байт. Определите объем памяти в байтах, необходимый для хранения 30 автомобильных номеров.

Решение

Вот что важно отметить: здесь чётко сказано, что первый символ — это буква, а остальные семь мест занимают исключительно цифры. Это даёт возможность немного оптимизировать решение. Вместо одной большой общей кодировки для всех символов мы можем разделить процесс и создать отдельные схемы кодирования для букв и цифр.

Итак, первый символ выбирается из 26 возможных вариантов, следовательно, потребуется минимум пять бит для его представления. Остальные места заполняются цифрами от нуля до девяти включительно, соответственно, каждому такому месту достаточно четырёх бит.

Получается такая схема: 5 + 4 × 7 = 33 бита на один номер. Поскольку число бит должно быть кратно восьми (для удобства перевода в байты), округлим вверх до ближайшего целого числа байт — получим ровно пять байт на один номер.

Теперь рассчитываем общий объём памяти для тридцати номеров: 30 × 5 = 150 байт.

Ответ: 150

Задание №10 (2058)

Сотрудникам компании выдают электронную карту, на которой записаны их личный код, номер подразделения (целое число от 1 до 120) и дополнительная информация. Личный код содержит 11 символов и может включать латинские буквы (заглавные и строчные буквы различаются) и десятичные цифры. Для хранения кода используется посимвольное кодирование, все символы кодируются одинаковым минимально возможным количеством битов, для записи кода отводится минимально возможное целое число байтов. Номер подразделения кодируется отдельно и занимает минимально возможное целое число байтов. Известно, что на карте хранится всего 28 байтов данных. Сколько байтов занимает дополнительная информация?

Решение

Во-первых, определимся с объемом объемом кода. Используемый алфавит включает заглавные и прописные латинские буквы (всего 52 варианта) плюс 10 цифр, итого получается 62 возможных знака. Чтобы представить любой из этих символов уникальным набором бит, нам понадобится 6 бит на символ (2⁶=64), потому что 62 < 64. Поскольку длина кода равна 11 знакам, общее количество необходимых бит составит 11*6=66. Разделив на 8 (бит в одном байте), получим около 8,25 байт. Однако, округляем до ближайшего большего целого значения — выходит 9 байт.

Далее перейдем к номеру отдела. Нужно сохранить любое значение от 1 до 120. видим, что 2⁷=128, следовательно, достаточно использовать 7 бит для представления любого номера отдела. Тем не менее, поскольку память распределяется целыми байтами, здесь необходим хотя бы 1 полный байт.

Таким образом, личный код занял 9 байт, а номер отдела еще 1 байт. Тогда оставшийся объем памяти отведён под дополнительную информацию. Рассчитаем её размер: вычтем уже занятые байты из общего объема карты

28-(9+1)=18.

Следовательно, именно столько, 18 байт, приходится на дополнительную информацию.

Ответ : 18

Вступление.

Мы начали курс с аналитического подхода, решая задачи «вручную», но теперь переходим к программному решению. Оно особенно полезно, когда формулировки сложные — например, нужно найти минимальную длину, кодировку, идентификатор и т.д. Там, где вручную нужно долго анализировать, программа справляется простым перебором. Такой подход подходит и для сложных, и для обычных задач, при этом код получается коротким, понятным и эффективным.

Задача № 1

(ЕГЭ-2022) При регистрации в компьютерной системе каждому объекту присваивается идентификатор, состоящий из 252 символов и содержащий только десятичные цифры и символы из 1700-символьного специального алфавита. В базе данных для хранения каждого идентификатора отведено одинаковое и минимально возможное целое число байт. При этом используется посимвольное кодирование идентификаторов, все символы кодируются одинаковым и минимально возможным количеством бит. Определите объём памяти (в Кбайт), необходимый для хранения 4096 идентификаторов. В ответе запишите только целое число – количество Кбайт.

Решение

Вспомним ход аналитического решения этой задачи. Сначала определим размер кодировки: используются десятичные цифры (10) и 1700 символов из специального алфавита. Всего 1710 символов. Зная размер кодировки, можно определить размер символа в битах, как показатель степени двойки, которая покрывает полностью размер кодировки. Для 1710 символов размер символа равен 11 бит (2¹⁰ = 1024 – это мало, меньше, чем 1710, 2¹¹ = 2048, этого достаточно, это больше, чем 1710).

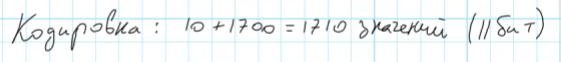
Далее вычисляем размер идентификатора в байтах, для этого умножаем размер идентификатора (количество символов в идентификаторе) из условия на вычисленный размер символа в битах и делим на 8 (для перевода в байты, 1 байт = 8 бит), затем получившийся результат округляем вверх до целого:

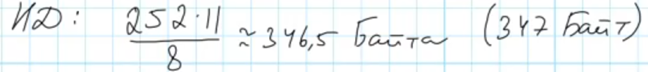
Для определения объёма памяти (в Кбайт), необходимого для хранения 4096 идентификаторов, умножим размер одного идентификатора в байтах на количество идентификаторов из условия и поделим на 1024 (для перевода в Кбайт, 1Кбайт = 1024 Байт):

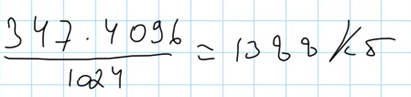
Получили ответ, объём памяти, необходимый для хранения 4096 идентификаторов, равен 1388.

Теперь решим эту же задачу с помощью программы. Открываем терминал IDLE, но программу в нем не пишем, потому что он не предназначен для написания полноценных программ, его можно использовать как калькулятор, для вычислений в одну — три строки. В IDLE выбираем File -> New file, открывается блокнот, и уже в нем мы будем писать программу. Терминал IDLE можно закрыть.

Прежде чем писать программу, действия, нам нужно импортировать две операции, которых нет по умолчанию в стандартном Python, это функция поиска логарифма по основанию 2, двоичного логарифма, и функция округления вверх до целого:

Импортируем из библиотеки math эти функции, пишем:

from math import log2, ceil

Можно для простоты импортировать сразу все функции из библиотеки math – писать:

from math import *

Определим кодировку, состоящую по условию из состоящую по условию из десятичной цифры (10) плюс 1700 символов:

кодировка = 10+1700

Определим размер символа в битах – округленный вверх двоичный логарифм из размера идентификатора кодировки:

бит = ceil( log2(кодировка) )

Размер идентификатора в байтах – это округленный в большую сторону размер 252 символов в битах, деленный на 8:

ид = ceil( 252*бит/8 )

Выводим на экран ответ на вопрос задачи — объём памяти (в байтах), необходимый для хранения 1096 идентификаторов:

print (ид*4096/1024)

Текст программы полностью:

from math import log2, ceil

кодировка = 10+1700

бит = ceil( log2(кодировка) )

ид = ceil( 252*бит/8 )

print(ид*4096/1024)

Запускаем, нажимая кнопку Run, либо клавишу f5, сохраняем программу и потом получаем результат:

Объём памяти (в байтах), необходимый для хранения 4096 идентификаторов, равен 1388.

Ответ: 1388

Вспомним, как в Python можно закомментировать кусок кода – выделить его и надать сочетание клавиш Alt + F3, а раскомментировать – выделить закомментированный текст и нажать Alt + F. Комментарии обозначаются знаком # и не играют роли в программе.

Задача №2

(А. Рогов) При регистрации в компьютерной системе каждому объекту присваивается идентификатор, состоящий из 213 символов и содержащий только десятичные цифры и символы из 1780-символьного специального алфавита. В базе данных для хранения каждого идентификатора отведено одинаковое и минимально возможное целое число байт. При этом используется посимвольное кодирование идентификаторов, все символы кодируются одинаковым и минимально возможным количеством бит. Кроме собственно идентификатора, для каждого пользователя в системе хранятся дополнительные сведения, для чего выделено целое число байт, одинаковое для всех пользователей. Для хранения сведений о 297 пользователях потребовалось 130 680 байт. Сколько байт выделено для хранения дополнительных сведений об одном пользователе?

Решение

Импортируем из библиотеки math нужные нам функции – для простоты импортируем всё, пишем:

from math import *

Определим кодировку, состоящую по условию из десятичной цифры (10) плюс 1780 символов:

кодировка = 10+1780

бит = ceil( log2(кодировка) )

Размер идентификатора в байтах – это округленный в большую сторону размер 213 символа в битах, деленный на 8:

ид = ceil( 213*бит/8 )

Определим объем памяти, выделенный для хранения сведений об одном пользователе – поделим объем памяти, необходимый для хранения сведений о 297 пользователях на 297:

юзер = 130_680/297

Выведем на экран ответ на вопрос задачи – разность между объемом памяти, необходимым для хранения всех данных об одном пользователе и размером идентификатора:

print(юзер - ид)

Текст программы полностью:

from math import *

кодировка = 10+1780

бит = ceil( log2(кодировка) )

ид = ceil( 213*бит/8 )

юзер = 130_680/297

print(юзер — ид)

Запускаем, получаем результат:

Для хранения дополнительных сведений об одном пользователе выделено 147 байт.

Ответ: 147

Задача № 3

Решение

Импортируем из библиотеки math нужные нам функции – для простоты импортируем всё, пишем:

from math import *

Определим кодировку, состоящую по условию из прописных и строчных букв латинского алфавита (по 26 прописных и строчных символов):

kod = 26+26

bit = ceil( log2(kod) )

Размер пароля в байтах – это округленный в большую сторону размер 7 символа в битах, деленный на 8:

pas = ceil(7*bit/8)

Определим объем памяти, необходимый для хранения всех данных о пользователе (пароль и 12 байт дополнительных сведений):

user = pas + 12

Выведем на экран ответ на вопрос задачи – наибольшее количество пользователей, о которых может быть сохранена информация в системе – для этого переведем 2Кб выделенной памяти в байты (2*1024), а затем поделим значение на объем памяти, необходимый для хранения всех данных о пользователе:

print(2*1024/user)

Текст программы полностью:

from math import *

kod = 26+26

bit = ceil( log2(kod) )

pas = ceil(7*bit/8)

user = pas + 12

print(2*1024/user)

Запускаем программу, получаем результат:

Поскольку не предусмотрено хранение информации о части пользователя, то в ответе указываем целую часть от полученного числа.

Наибольшее количество пользователей, о которых может быть сохранена информация в системе, равно 113.

Ответ: 113

Задача №4

На предприятии каждой изготовленной детали присваивают серийный номер, содержащий десятичные цифры, 52 латинские буквы (с учётом регистра) и символы из 458-символьного специального алфавита. В базе данных для хранения каждого серийного номера отведено одинаковое и минимально возможное целое число байт. При этом используется посимвольное кодирование серийных номеров, все символы кодируются одинаковым и минимально возможным числом бит. Известно, что для хранения 862 серийных номеров отведено не более 276 Кбайт памяти. Определите максимально возможную длину серийного номера. В ответе запишите только целое число.

Решение

Импортируем из библиотеки math нужные нам функции – для простоты импортируем всё, пишем:

from math import *

Запускаем цикл по возможной длине серийного номера l (от 1 до 1000). Число 1000 в цикле берется примерное, если окажется, что длина равна 1000, то увеличим это число.

Мы ищем минимальное подходящее значение, поэтому цикл идёт по возрастанию:

for l in range(1,1000)

Определим кодировку, состоящую по условию из десятичных цифр, прописных и строчных букв латинского алфавита (52 символа), а также 458 символов из специального алфавита:

kod = 10+52+458

bit = ceil (log2(kod) )

Размер серийного номера в байтах – это округленный в большую сторону размер l символов в битах, деленный на 8:

nom = ceil(l*bit/8)

Проверяем, будет ли общий объём памяти не больше 276 Кбайт (276 Кбайт = 276 * 1024 байт), если у нас 862 номера, каждый из которых занимает nom байт:

if 862*nom <= 276*1024

Если условие выполняется, мы нашли возможную длину l, при которой объём не превышает 276Кб, выводим её на экран:

print(l)

Текст программы полностью:

from math import *

for l in range(1,1000):

kod = 10+52+458

bit = ceil(log2(kod))

nom = ceil(l*bit/8)

if 862*nom <= 276*1024:

print(l)

Запускаем программу, получаем результат:

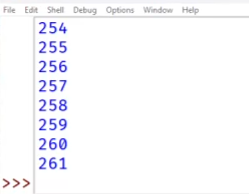
Мы перебирали последовательно длины серийного номера, начинающиеся с 2 и получали, что до 261 символа на номер, для хранения 862 серийных номеров нужно не более 2Кб памяти. Длины более 261 символа на номер не подходят, в этих случаях объем памяти превысит заданный.

Максимально возможна длина серийного номера равна 261.

Ответ: 261.

Задача №5

На предприятии каждой изготовленной детали присваивают серийный номер, состоящий из 261 символов. Для его хранения отведено одинаковое и минимально возможное целое число байт. При этом используется посимвольное кодирование серийных номеров, все символы кодируются одинаковым и минимально возможным числом бит. Известно, что для хранения 252 500 серийных номеров отведено более 31 Мбайт памяти. Определите минимально возможную мощность алфавита, из которого составляются серийные номера. В ответе запишите только число.

Решение

Импортируем из библиотеки math нужные нам функции – для простоты импортируем всё, пишем:

from math import *

Запускаем цикл по возможному количеству разных символов одного серийного номера kod (от 1 до 999).

Мы ищем минимальное подходящее значение, поэтому цикл идёт по возрастанию:

for kod in range (1,1000)

bit = ceil( log2(kod) )

Размер серийного номера в байтах – это округленный в большую сторону размер 261 символов в битах, деленный на 8:

nom = ceil(261*bit/8)

Считаем, сколько всего байт потребуется для хранения всех номеров (252500 серийных номеров по nom байт каждый: 252_500*nom), и проверяем превышает ли это 31 Мбайт (это 31*1024*1024 байт):

if 252_500*nom > 31*1024*1024

Если условие выполняется, мы нашли значение kod, выводим его на экран и выходим из цикла:

print(kod)

Текст программы полностью:

from math import *

for kod in range(1,1000):

bit = ceil( log2(kod) )

nom = ceil(261*bit/8)

if 252_500*nom > 31*1024*1024:

print(kod)

break

Запускаем программу, получаем результат:

Получили список возможных мощностей алфавита, при котором 252 500 серийных номеров занимают более 31 Мбайт памяти. Поскольку в задаче требуется узнать минимальную мощность алфавита, в ответе указываем число 9.

Для того, чтобы не перебирать все числа, а вывести сразу одно минимальное, в конце программы допишем команду break. В этом случае программа выведет одно минимальное подходящее число – ответ на задачу, и будет прервана:

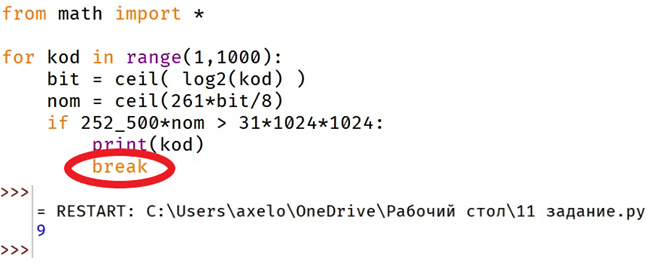
Минимально возможная мощность алфавита равна 9.

Ответ: 9

Задача №6

На складе каждой упаковке товара присваивают уникальный идентификатор, который может содержать десятичные цифры, 26 латинских букв (без учёта регистра) и символы из 476-символьного специального алфавита. В базе данных для хранения каждого идентификатора отведено одинаковое и минимально возможное целое число байт. При этом используется посимвольное кодирование идентификаторов, все символы кодируются одинаковым и минимально возможным числом бит. Известно, что для хранения 5000 идентификаторов отведено не более 1 Мбайт памяти. Определите максимально возможную длину идентификатора. В ответе запишите только целое число.

Решение

Импортируем из библиотеки math нужные нам функции – для простоты импортируем всё, пишем:

from math import *

Запускаем цикл по возможной длине серийного номера l (от 1 до 9999).

Мы ищем максимальное подходящее значение, поэтому цикл идёт по убыванию:

for l in range (10000,1,-1)

Определим кодировку, состоящую по условию из десятичных цифр, букв латинского алфавита (26 символов), а также 476 символов из специального алфавита:

kod = 10+26+476

bit = ceil(log2(kod))

Размер серийного номера в байтах – это округленный в большую сторону размер l символов в битах, деленный на 8:

idd = ceil(l*bit/8)

Проверяем, помещаются ли все 5000 идентификаторов, каждый по idd байт, в 1 Мбайт (1 Мбайт = 1*1024* 1024 байт):

if 5000*idd <= 1*1024*1024

Если условие выполняется, мы нашли максимальную длину l, при которой объём не превышает 1 Мбайт, выводим её на экран:

print(l)

и выходим из цикла:

break

Текст программы полностью:

from math import *

for l in range(10000,1,-1):

kod = 10+26+476

bit = ceil(log2(kod))

idd = ceil(l*bit/8)

if 5000*idd <= 1*1024*1024:

print(l)

break

Запускаем программу, получаем результат:

Максимально возможная длина идентификатора равна 185 символам.

Ответ: 185

Задача № 7

Каждое изделие, изготовленное на предприятии, получает уникальный код, состоящий из 30 символов. Каждый символ кода может быть латинской буквой (заглавной или строчной), десятичной цифрой или специальным символом из особого технического набора. В базе данных хранится список всех уже использованных кодов. При этом используется посимвольное кодирование, каждый символ кодируется одинаковым минимально возможным числом бит, а для хранения каждого кода отводится одинаковое минимально возможное число байт. Известно, что для хранения списка из 5200 кодов выделено не более 150 Кбайт. Какое наибольшее количество специальных символов может входить в особый технический набор?

Решение

Импортируем из библиотеки math нужные нам функции – для простоты импортируем всё, пишем:

from math import *

Запускаем цикл по возможному количеству количество специальных символов в наборе nabor (от 2 до 999).

Мы ищем максимальное подходящее значение, поэтому цикл идёт по убыванию:

for nabor in range(1000,1,-1)

Определим кодировку, состоящую по условию прописных (26) и строчных букв (26) латинского алфавита, из десятичных цифр, а также некоторого количества специальных символов, равного nabor:

kod = 26+26+10+nabor

bit = ceil(log2(kod))

Размер кода в байтах – это округленный в большую сторону размер 30 символов в битах, деленный на 8:

idd = ceil(30*bit/8)

Считаем, сколько всего байт потребуется для хранения всех кодов (5200 идентификаторов по idd байт каждый: 5200*idd), и проверяем меньше ли это число, чем отведенные 150Кбайт (это 150*1024 байт):

if 5200*idd <= 150*1024

Если условие выполняется, мы нашли максимальное значение nabor, выводим его на экран и выходим из цикла:

print(nabor) / break

Текст программы полностью:

from math import *

for nabor in range(1000,1,-1):

kod = 26+26+10+nabor

bit = ceil(log2(kod))

idd = ceil(30*bit/8)

if 5200*idd <= 150*1024:

print(nabor)

break

Запускаем программу, получаем результат:

Наибольшее количество специальных символов, которое может входить в особый технический набор, равно 66.

Ответ: 66.

Задача №8

На предприятии каждой изготовленной детали присваивают серийный номер, состоящий из 119 символов. В базе данных для хранения каждого серийного номера отведено одинаковое и минимально возможное число байт. При этом используется посимвольное кодирование серийных номеров, все символы кодируются одинаковым и минимально возможным числом бит. Известно, что 125 300 серийных номеров занимают более 23 Мбайт памяти. Определите минимально возможную мощность алфавита, используемого для записи серийных номеров. В ответе запишите только целое число.

Решение

Импортируем из библиотеки math нужные нам функции – для простоты импортируем всё, пишем:

from math import *

Запускаем цикл по возможному количеству разных символов одного серийного номера kod (от 1 до 9999).

Мы ищем минимальное подходящее значение, поэтому цикл идёт по возрастанию:

for kod in range(1,10000)

bit = ceil(log2(kod))

Размер серийного номера в байтах – это округленный в большую сторону размер 119 символов в битах, деленный на 8:

nom = ceil(119*bit/8)

Считаем, сколько всего байт потребуется для хранения всех номеров (125_300 серийных номеров по nom байт каждый: 125_300*nom), и проверяем является ли это не менее 23 Мбайт (это 23*1024*1024 байт):

if 125_300*nom>23*1024*1024

Если условие выполняется, мы нашли минимальное значение kod, выводим её на экран:

print(kod)

и выходим из цикла:

break

Текст программы полностью:

from math import *

for kod in range(1,10000):

bit = ceil(log2(kod))

nom = ceil(119*bit/8)

if 125_300*nom>23*1024*1024:

print(kod)

break

Запускаем программу, получаем результат:

Минимально возможная мощность алфавита равна 4097.

Ответ: 4097

Задача №9

В медицинском учреждении каждой медицинской карточке пациента присваивают уникальный идентификатор, состоящий из 20 символов. Для его хранения отведено одинаковое и минимально возможное целое число байт. При этом используется посимвольное кодирование идентификаторов, все символы кодируются одинаковым и минимально возможным числом бит. Известно, что для хранения 600 000 идентификаторов отведено более 11 Мбайт памяти. Определите минимально возможную мощность алфавита, который используется для составления идентификаторов. В ответе запишите только число.

Решение

Импортируем из библиотеки math нужные нам функции – для простоты импортируем всё, пишем:

from math import *

Запускаем цикл по возможному количеству разных символов одного идентификатора kod (от 2 до 999999).

Мы ищем минимальное подходящее значение, поэтому цикл идёт по возрастанию

for kod in range(1,1000000)

bit = ceil(log2(kod))

Размер идетификатора в байтах – это округленный в большую сторону размер 23 символов в битах, деленный на 8:

idd = ceil(23*bit/8)

Считаем, сколько всего байт потребуется для хранения всех номеров (600000 идентификаторов по idd байт каждый: 600_000*idd), и проверяем меньше ли это число, чем отведенные 11 Мбайт (это 11*1024*1024 байт):

if 600_000*idd > 11*1024*1024

Если условие выполняется, мы нашли максимальное значение kod, выводим его на экран и выходим из цикла:

print(kod) / break

Текст программы полностью:

from math import *

for kod in range(1,1000000):

bit = ceil(log2(kod))

idd = ceil(20*bit/8)

if 600_000*idd > 11*1024*1024:

print(kod)

break

Запускаем программу, получаем результат:

Минимальная возможная мощность алфавита равна 129.

Ответ: 129

Номер 11. ЕГЭ по информатике

Ещё номера