Некоторые рекомендации о том, как описать проект.
Условие задачи:
Миша заполнял таблицу истинности логической функции F
но успел заполнить лишь фрагмент из трёх различных её строк, даже
не указав, какому столбцу таблицы соответствует каждая из переменных
w, x, y, z.
Определите, какому столбцу таблицы соответствует каждая из переменных
w, x, y, z.
В ответе напишите буквы w, x, y, z в том порядке, в котором идут
соответствующие им столбцы (сначала буква, соответствующая первому
столбцу; затем буква, соответствующая второму столбцу, и т.д.). Буквы
в ответе пишите подряд, никаких разделителей между буквами ставить
не нужно.
Решение:
Смотрим и замечаем, что у нас два действия И и результат в таблице ИСТИНА во всех случаях, отсюда делаем вывод, что всех 3 части выражения должны быть истиной, т.е. 1 И 2 И 3 = 1. Последнее выражение упрощает поиск, NOT W должно быть истиной, значит W должно быть ложью, соответственно W можно поставить только в 4 столбик.
Разберем вторую скобку (там проще). Она должны быть истинна, соответственно YZ не может стоять в позициях 1,3 и 2,3, остается 1 вариант 1,2. Отсюда получаем, что X будет на 3 позиции. И укажем сразу, что Y и Z должны быть разными.
Также если посмотреть на таблицу (а в таблице не может быть одинаковых строк), то оставшееся место для Х будет 0.
От заполненной таблицы можем определить, что Y будет на 2 позиции. Почему? Потому что по первой скобке выражения, чтобы получилась ИСТИНА, нужно чтобы хотя бы одна из переменных должна быть истиной, а такое невозможно (по строке 2 таблицы), если Y будет на 1 позиции.
То есть Х у нас должен быть всегда 0, отсюда делаем вывод, что Х стоит в третьем столбце и всегдя будет 0.
Соответственно, получаем ответ zyxw.
Ответ:
ZYXW
Решение в Python.
Программа, которая выдает готовый ответ:
Логика, алгебра логики.


Алгебра логики лежит в основе логических схем и операций, из которых состоят все вычисления в компьютерах: все компьютерные операции — это комбинации логических операций. Алгебра логики — это формализованная система, основанная на работе с 0 и 1, которая позволяет описывать вычисления и логические схемы. Она — основа цифровой логики и программирования.
В обычной алгебре мы работаем с переменными, которые могут принимать различные числовые значения: натуральные, целые, рациональные, иррациональные и так далее. Это — произвольные величины, неизвестные числа, с которыми проводятся математические операции.
В алгебре логики вместо переменных используются высказывания. Они играют ту же роль — могут принимать значения, но не любые, а строго два:
· 1 — соответствует истине
· 0 — соответствует лжи
Таким образом, высказывания — это аналог переменных, но с ограниченным набором значений.
Также как и в математике, где существуют операции (сложение, вычитание, умножение, деление, возведение в степень, логарифмы и т.д.), в алгебре логики есть логические операции:
· НЕ (отрицание)
· И (конъюнкция)
· ИЛИ (дизъюнкция)
· импликация (если… то…)
· эквивалентность (равнозначность)
И в математике, и в алгебре логики есть функции — только в первом случае это функции над числами, а во втором — над логическими значениями (0 и 1).
По сути, алгебра логики — это аналог обычной алгебры, но в ней:
· используются не числа, а только ноль и единица
· переменными являются высказывания
· операции — это логические связки
Причём в логике часто даже отказываются от привязки к понятиям «правда» и «ложь», и просто говорят: есть 0 и 1. Это позволяет рассматривать логику абстрактно, как математическую систему, независимо от смысла.

В рамках ЕГЭ по информатике используются пять логических операций:
1. Отрицание (НЕ):
o Обозначается: ¬A или not A (в Python: not)
o Меняет значение на противоположное:
¬0 = 1, ¬1 = 0
2. Конъюнкция (И):
o Обозначается: A ∧ B, A * B, в ЕГЭ — «галочка вверх»
o В Python: and
o Результат 1, только если оба операнда равны 1
1 ∧ 1 = 1, остальные случаи — 0
3. Дизъюнкция (ИЛИ):
o Обозначается: A ∨ B, A + B, в ЕГЭ — «галочка вниз»
o В Python: or
o Результат 0, только если оба операнда равны 0
0 ∨ 0 = 0, остальные — 1
4. Импликация (ЕСЛИ…ТО):
o Обозначается: A → B, в Python заменяется на A <= B
o Основное правило:
1 → 0 = 0 (это единственный случай, когда результат — ложь)
Остальные — истина
o Запомнить можно по аналогии:
«Начальник сказал (1), работник не сделал (0) — плохо (ложь)»
5. Эквиваленция (ТОГДА И ТОЛЬКО ТОГДА)
o Обозначается: A ≡ B или A = = B
o В Python — заменяется на A = = B
o Результат 1, если значения одинаковые
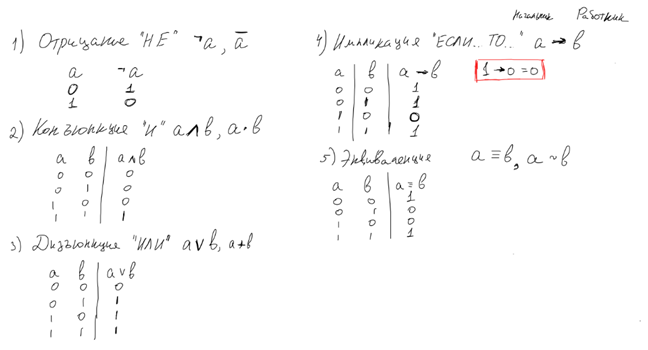
В Python реализованы напрямую три операции – отрицание, конъюнкция и дизъюнкция. Импликация и эквиваленция напрямую не реализованы. Импликация (→) заменяется на « <= », Эквиваленция (≡) → заменяется на « == ». Эти замены работают только с 0 и 1, и лишь в логическом смысле, но формально — это другие операции с другим приоритетом.
Приоритет операций
В логике:
1. NOT (not)
2. AND (and)
3. OR (or)
4. Импликация (→)
5. Эквиваленция (≡)
В Python:
- приоритет » <= «, » == » выше, чем and, or, not
Python может неправильно интерпретировать выражения с « <= » или « == », потому что приоритет этих операций выше, чем у логических. Поэтому нужно явно ставить скобки, чтобы задать нужный порядок операций.

Таблицы истинности
Таблица истинности — это способ посмотреть, как логическая функция ведёт себя при всех возможных значениях переменных.
Например, у нас есть логическая функция f=(x∧y∧z)∨(⇁x∧y∧⇁z)∨(x∧⇁y∧z)f=(x∧y∧z)∨(⇁x∧y∧⇁z)∨(x∧⇁y∧z) Таблица истинности показывает все возможные комбинации значений x, y, z (только 0 и 1) и соответствующее значение f для каждой комбинации.
Как построить таблицу истинности в Python:
1. Выводим заголовок:
print(‘x y z’)
2. Перебираем все возможные комбинации значений:
for x in 0,1:
for y in 0,1:
for z in 0,1:3. Считаем значение функции для каждой комбинации:
f = (x and y and z) or (not x and y and not z) or \
(x and not y and z)
4. Выводим результат, преобразуя True/False в 1/0 (int(f) используется, чтобы вместо True и False печатались привычные 1 и 0.):
print(x, y, z, int(f))
Таблица позволяет увидеть, в каких случаях функция равна 1, а в каких — 0. Иногда важны только строки, где f = 1 или f = 0, можно добавить условие:
if f==1:
print(x,y,z)

Задача № 1 (53)
Логическая функция F задаётся выражением (¬x ∧ y ∧ z) ∨ (¬x ∧ ¬z). На рисунке приведён фрагмент таблицы истинности функции F, содержащий все наборы аргументов, при которых функция F истинна. Определите, какому столбцу таблицы истинности функции F соответствует каждая из переменных x, y, z.
В ответе напишите буквы x, y, z в том порядке, в котором идут соответствующие им столбцы (без разделителей).
Решение
Напишем программу, выведем таблицу значений для x,y,z. Выводим на экран заголовок таблицы:
print(‘x y z’)
Перебираем в цикле значения для всех переменных – 0 и 1:
:
for x in 0,1:
for y in 0,1:
for z in 0,1:Для каждого набора значений вычисляется результат для функции F из условия задачи:
f = (not x and y and z) or (not x and not z)
Если функция истинна, выводим на экран соответствующие значения переменных:
if f==1:
print(x,y,z)Текст программы полностью:
print('x y z')
for x in 0,1:
for y in 0,1:
for z in 0,1:
f = (not x and y and z) or (not x and not z)
if f==1:
print(x,y,z)Запускаем программу, получаем таблицу значений переменных функции f, в том случае, если она равна единице.

Сравниваем её столбцы с таблицей из условия задачи: переменная х принимает значения только равные нулю, следовательно, ей соответствует второй столбец из таблицы в условии задачи, переменная z два раза принимает значение, равное нулю и один раз – единице, следовательно, ей соответствует первый столбец. Оставшийся второй столбец соответствует переменной у.
В ответе на задачу указываем zxy.
Ответ: zxy
Задача №2 (3648)
Логическая функция F задаётся выражением (a → d) ∧ ¬(b → c).
На рисунке приведён частично заполненный фрагмент таблицы истинности функции F, содержащий неповторяющиеся строки. Определите, какому столбцу таблицы истинности функции F соответствует каждая из переменных a, b, c, d.
Решение
Напишем программу, выведем таблицу значений для a,b,c,d если логическая функция F истинна. Выводим на экран заголовок таблицы:
print(‘a b c d’)
Перебираем в цикле значения для всех переменных – 0 и 1:
for a in 0,1:
for b in 0,1:
for c in 0,1:
for d in 0,1:Для каждого набора значений вычисляется результат для функции F из условия задачи:
f = (a <= d) and not(b<=c)
Если функция истинна, выводим на экран соответствующие значения переменных:
if f==1:
print(a,b,c,d)Текст программы полностью:
print('a b c d')
for a in 0,1:
for b in 0,1:
for c in 0,1:
for d in 0,1:
f = (a <= d) and not(b<=c)
if f==1:
print(a,b,c,d)Запускаем программу, получаем таблицу значений переменных функции f, в том случае, если она равна единице.

Сравниваем её столбцы с таблицей из условия задачи: переменная c принимает значения только равные нулю, следовательно, ей соответствует четвертый столбец из таблицы в условии задачи, переменная b принимает значения только равные единице, ей соответствует третий столбец, переменная a два раза принимает значение, равное нулю и один раз – единице, следовательно, ей соответствует второй столбец. Оставшийся первый столбец соответствует переменной d.
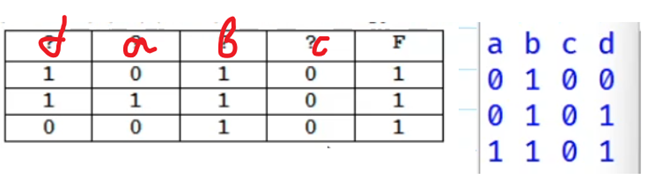
Записываем в ответе dabc.
Ответ: dabc
Задача 3 (55)
Логическая функция F задаётся выражением (a → b) ∧ ((a ∧ b) → ¬c). Определите, какому столбцу таблицы истинности функции F соответствует каждая из переменных a, b, c.
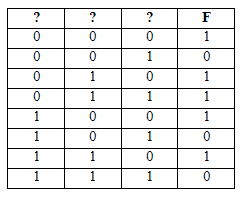
В ответе напишите буквы a, b, c в том порядке, в котором идут соответствующие им столбцы (без разделителей).
Решение
Попробуем получить результат не используя всю таблицу значений для функции, а возьмем только ту её часть, где f = 0.
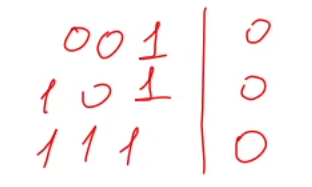
Напишем программу, выведем таблицу значений для a, b, c если логическая функция F ложна. Выводим на экран заголовок таблицы:
print(‘a b c’)
Перебираем в цикле значения для всех переменных – 0 и 1:
for a in 0,1:
for b in 0,1:
for c in 0,1:Для каждого набора значений вычисляется результат для функции F из условия задачи:
f = (a<=b) and ((a and b) <= (not c))
Если функция ложна, выводим на экран соответствующие значения переменных:
if f==0:
print(a,b,c)Обратим внимание на расстановку скобок. Если не поставить их правильным образом, программа выдаст ошибку:
Текст программы полностью:
print('a b c')
for a in 0,1:
for b in 0,1:
for c in 0,1:
f = (a<=b) and ((a and b) <= (not c))
if f==0:
print(a,b,c)Запускаем программу, получаем таблицу значений переменных, при которых функция принимает значение, равное нулю.

Сравниваем её с данными из таблицы в условии задачи и получаем ответ. Первый столбец соответствует переменной с (две единицы и ноль), второй столбец – переменной b (два ноля и единица) и третий столбец – переменной a (три единицы).
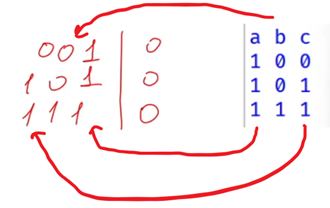
В ответе на задачу указываем cba.
Ответ: cba
Задача № 4 (1636)
Логическая функция F задаётся выражением (x ∨ y) ∧ ¬(y ≡ z) ∧ ¬w.
На рисунке приведён частично заполненный фрагмент таблицы истинности функции F, содержащий неповторяющиеся строки. Определите, какому столбцу таблицы истинности функции F соответствует каждая из переменных x, y, z, w.
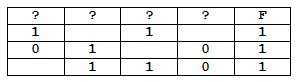
Решение
Напишем программу, выведем таблицу значений для x,y,w,z если логическая функция F истинна. Выводим на экран заголовок таблицы:
print(‘x y z w’)
Перебираем в цикле значения для всех переменных – 0 и 1:
for x in 0,1:
for y in 0,1:
for w in 0,1:
for z in 0,1:Для каждого набора значений вычисляется результат для функции F из условия задачи:
f = (x or y) and not (y==z) and not w
Если функция истинна, выводим на экран соответствующие значения переменных:
if f==1:
print(x,y,w,z)Текст программы полностью:
print('x y w z')
for x in 0,1:
for y in 0,1:
for w in 0,1:
for z in 0,1:
f = (x or y) and not (y==z) and not w
if f==1:
print(x,y,w,z)Запускаем программу, получаем таблицу значений переменных, при которых функция f принимает значение, равное единице.

Сравниваем её с таблицей из условия задачи. Переменной w однозначно соответствует четвертый столбец, так как только в нем могут стоять три ноля, в других столбцах уже есть хотя бы одна единица. Переменной z соответствует первый столбец, потому что она два раза принимает значения, равные нулю и один раз – единице, а в других столбцах стоят по две единицы. Чтобы определить столбец, соответствующий переменной x, обратим внимание на вторую строку в получившейся таблице. При z = 1, x = 1, а y = 0. Такая ситуация описывается первой строкой в таблице из условия задачи, отсюда получаем, что х соответствует третий столбец, а у – второй.
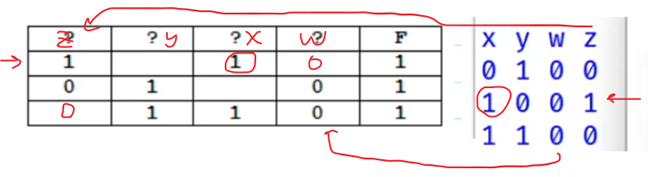
В ответе на задачу записываем zyxw.
Ответ: zyxw
Задача №5 (8151)
Логическая функция F задаётся выражением w ∧ ¬((x → y) → (y ≡ z)). На рисунке приведён частично заполненный фрагмент таблицы истинности функции F, содержащий неповторяющиеся строки. Определите, какому столбцу таблицы истинности функции F соответствует каждая из переменных x, y, z, w.
В ответе напишите буквы x, y, z, w в том порядке, в котором идут соответствующие им столбцы. Буквы в ответе пишите подряд, никаких разделителей между буквами ставить не нужно.
Решение
Напишем программу, выведем таблицу значений для x,y,w,z если логическая функция F истинна. Выводим на экран заголовок таблицы:
print(‘x y z w’)
Перебираем в цикле значения для всех переменных – 0 и 1:
for x in 0,1:
for y in 0,1:
for w in 0,1:
for z in 0,1:Для каждого набора значений вычисляется результат для функции F из условия задачи:
f = w and not((x<=y) <= (y==z))
Если функция истинна, выводим на экран соответствующие значения переменных:
if f==1:
print(x,y,w,z)Текст программы полностью:
print('x y w z')
for x in 0,1:
for y in 0,1:
for w in 0,1:
for z in 0,1:
f = w and not((x<=y) <= (y==z))
if f==1:
print(x,y,w,z)Запускаем программу, получаем таблицу значений переменных, при которых функция f принимает значение, равное единице.

Сравниваем её с таблицей из условия задачи. Переменной w однозначно соответствует третий столбец, так как только в нем могут стоять три единицы, в других столбцах уже есть хотя бы один ноль. Обратим внимание на то, что во всех строках в получившейся таблицы есть хотя бы один ноль, следовательно, в первом столбце в третьей строке должен стоять ноль. Выходит, что первый столбец соответствует переменной z, потому что она два раза принимает значения, равные нулю и один раз – единице, а в других столбцах стоят по две единицы. Четвертый столбец в заданной таблице у нас определен полностью и соответствует x, следовательно, у соответствует второй столбец.
В ответе на задачу записываем zywx.
Ответ: zywx
Задача №6 (7511)
(ЕГЭ-2024) Логическая функция F задаётся выражением (y → ¬ (x → z))∨∨ w. На рисунке приведён частично заполненный фрагмент таблицы истинности функции F, содержащий неповторяющиеся строки. Определите, какому столбцу таблицы истинности функции F соответствует каждая из переменных x, y, z, w.
В ответе напишите буквы x, y, z, w в том порядке, в котором идут соответствующие им столбцы. Буквы в ответе пишите подряд, никаких разделителей между буквами ставить не нужно.
Решение
Напишем программу, выведем таблицу значений для x,y,w,z если логическая функция F ложна. Выводим на экран заголовок таблицы:
print(‘x y z w’)
Перебираем в цикле значения для всех переменных – 0 и 1:
for x in 0,1:
for y in 0,1:
for w in 0,1:
for z in 0,1:Для каждого набора значений вычисляется результат для функции F из условия задачи:
f = (y <= (not(x<=z)) ) or w
Если функция ложна, выводим на экран соответствующие значения переменных
if f==0:
print(x,y,w,z)Текст программы полностью:
print('x y w z')
for x in 0,1:
for y in 0,1:
for w in 0,1:
for z in 0,1:
f = (y <= (not(x<=z)) ) or w
if f==0:
print(x,y,w,z)Запускаем программу, получаем таблицу значений переменных, при которых функция f принимает значение, равное единице.

Сравниваем её с таблицей из условия задачи. Переменной y однозначно соответствует третий столбец, так как только в нем могут стоять три единицы, в других столбцах уже есть хотя бы один ноль. Заполняем этот столбец единицами. Переменной w может соответствовать только четвертый столбец, так она принимает значения только равные нулю, а в других столбцах присутствуют единицы. Заполним четвертый столбец в заданной таблице нулями. Обратим внимание на вторые строки в обеих таблицах – они одинаковы. Отсюда получим, что второй столбец соответствует переменной z, следовательно, оставшийся первый столбец соответствует переменной х.
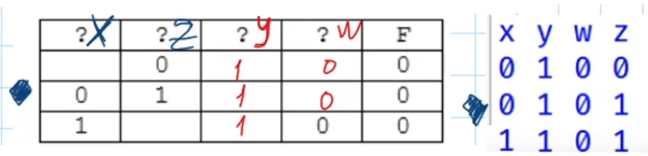
В ответе на задачу записываем xzyw.
Ответ: xzyw
Задача №7 (7902)
Логическая функция F задаётся выражением (x ≡ (y → z)) ∧ (y ≡ ¬(z → w)). На рисунке приведён частично заполненный фрагмент таблицы истинности функции F, содержащий неповторяющиеся строки. Определите, какому столбцу таблицы истинности функции F соответствует каждая из переменных x, y, z, w.
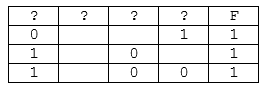
В ответе напишите буквы x, y, z, w в том порядке, в котором идут соответствующие им столбцы. Буквы в ответе пишите подряд, никаких разделителей между буквами ставить не нужно.
Решение
Напишем программу, выведем таблицу значений для x,y,w,z если логическая функция F истинна. Выводим на экран заголовок таблицы:
print(‘x y z w’)
Перебираем в цикле значения для всех переменных – 0 и 1:
for x in 0,1:
for y in 0,1:
for w in 0,1:
for z in 0,1:Для каждого набора значений вычисляется результат для функции F из условия задачи:
f = (x==(y<=z)) and (y == (not(z<=w)) )
Если функция истинна, выводим на экран соответствующие значения переменных:
if f==1
print(x,y,w,z)Текст программы полностью:
print('x y w z')
for x in 0,1:
for y in 0,1:
for w in 0,1:
for z in 0,1:
f = (x==(y<=z)) and (y == (not(z<=w)) )
if f==1:
print(x,y,w,z)Запускаем программу, получаем таблицу значений переменных, при которых функция f принимает значение, равное единице.

Сравниваем её с таблицей из условия задачи. Переменной х однозначно соответствует второй столбец, так как только в нем могут стоять все единицы, в других столбцах уже есть хотя бы один ноль. Заполняем этот столбец единицами. Обратим внимание на третью строку заданной таблицы и вторую строку получившейся – они одинаковы, в них по два нуля и две единицы. Отсюда получаем, что первый столбец соответствует переменной w. Посмотрим на четвертую получившейся таблицы: при x = 1 и w = 0, y = 1 и z = 1. Такими значениями можно заполнить первую строку заданной таблицы. Учитывая, что при x = 1 и w = 1 (третья строка получившейся таблицы), y = 0, а z = 1, получаем, что третий столбец соответствует у, а четвертый – z.

В ответе на задачу записываем wxyz.
Ответ: wxyz
Задача № 8 (3644)
Логическая функция F задаётся выражением ¬w ∧ (y ∨ z → ¬x ∧ y).

На рисунке приведён частично заполненный фрагмент таблицы истинности функции F, содержащий неповторяющиеся строки. Определите, какому столбцу таблицы истинности функции F соответствует каждая из переменных x, y, z, w.
Решение
Напишем программу, выведем таблицу значений для x,y,w,z если логическая функция F истинна. Выводим на экран заголовок таблицы:
print(‘x y z w’)
Перебираем в цикле значения для всех переменных – 0 и 1:
Для каждого набора значений вычисляется результат для функции F из условия задачи:
f = not w and ((y or z) <= (not x and y) )
Если функция истинна, выводим на экран соответствующие значения переменных:
Текст программы полностью:
print('x y w z')
for x in 0,1:
for y in 0,1:
for w in 0,1:
for z in 0,1:
f = not w and ((y or z) <= (not x and y) )
if f==1:
print(x,y,w,z)Запускаем программу, получаем таблицу значений переменных, при которых функция f принимает значение, равное единице.

Сравниваем её с таблицей из условия задачи. Исключим строку 0 0 0 0 в получившейся таблице, потому что в заданной такой строки нет. Переменной w однозначно соответствует первый столбец, так как только в нем могут стоять три ноля, в других столбцах уже есть хотя бы одна единица. Переменной у однозначно соответствует третий столбец, так как в нем есть две единицы, а переменные x и z принимают значение, равное единице, только один раз. Заполняем этот столбец в соответствии с полученными значениями для переменной у. Обратим внимание на третью строку заданной таблицы и третью строку получившейся – они одинаковы, в них по два нуля и две единицы. Отсюда получаем, что второй столбец соответствует переменной z, и, следовательно, оставшийся четвертый столбец соответствует переменной х.

В ответе на задачу записываем wzyx.
Ответ: wzyx
Задача №9 (6111)
Логическая функция F задаётся выражением w ∨ (y → z) ∧ x. На рисунке приведён частично заполненный фрагмент таблицы истинности функции F, содержащий неповторяющиеся строки. Определите, какому столбцу таблицы истинности функции F соответствует каждая из переменных x, y, z, w.

В ответе напишите буквы x, y, z, w в том порядке, в котором идут соответствующие им столбцы. Буквы в ответе пишите подряд, никаких разделителей между буквами ставить не нужно.
Решение
Для каждого набора значений вычисляется результат для функции F из условия задачи:
f = w or (y<=z) and x
По очереди запустим программу для f = 0 и f = 1. Если функция ложна, выводим на экран соответствующие значения переменных:
Если функция истинна, выводим на экран соответствующие значения переменных:
Текст программы полностью:
print('x y w z')
for x in 0,1:
for y in 0,1:
for w in 0,1:
for z in 0,1:
f = w or (y<=z) and x
if f==1:
print(x,y,w,z)Сравним две полученные таблицы значений, для f = 0 и f = 1, с таблицей из условия задачи:

В первую очередь оставляем только те строки, которые могут помочь. Из таблицы для f = 0 оставляем те, в которых по две единицы. Переменная w принимает значения, только равные 0, поэтому можем сделать вывод, что третий столбец в заданной таблице соответствует переменной w. Заполняем свободные клетки в этом столбце нулями.
Из таблицы для f = 1 исключаем строки, в которых w = 1, а так же те, в которых больше двух единиц (в заданной таблице строка для f = 1 уже заполнена двумя нулями). Рассмотрим оставшиеся строки в получившейся таблице для f = 0. Видим в них по две единицы и два нуля. Заполним этими значениями заданную таблицу. Обратим внимание, что для f=0 переменная у принимает значения, равные единице в обеих строках, следовательно, первый столбец в заданной таблице – это переменная у. Для f = 1 переменная у равна 0 в обеих оставшихся строках, укажем в первой строке для переменной у значение 0. Получили строку, в которой стоит три нуля. Следовательно, это первая из двух оставшихся строк в получившейся таблице для f = 1. В ней z = 0, следовательно, этой переменной соответствует четвертый столбец, а х = 1, ей соответствует второй столбец.

В ответе на задачу записываем yxwz.
Ответ: yxwz
Задача №10 (6992)
После заполнения трех таблиц истинности для трех логических функций, взяли ровно по одной строке из каждой таблицы.
Определите, какому столбцу таблицы соответствует каждая из переменных w,x,y,z.
В ответе запишите буквы w,x,y,z в том порядке, в котором идут соответствующие им столбцы (сначала буква, соответствующая первому столбцу; затем буква, соответствующая второму столбцу и т.д.). Буквы в ответе пишите подряд, никаких разделителей между буквами ставить не нужно.
Решение
Для каждого набора значений вычисляется результат для функций f1, f2, f3 из условия задачи:
f1 = (w<=y) == (x and z)
f2 = not x or not y or not z or w
f3 = (z or w) and y and x
По очереди запустим программу для f1 = 1, f2 = 0 и f3 = 1. Выводим на экран соответствующие значения переменных:
#if f1==1:
#if f2==0:
if f3==1:
print(x,y,w,z)Текст программы полностью:
print('x y w z')
for x in 0,1:
for y in 0,1:
for w in 0,1:
for z in 0,1:
f1 = (w<=y) == (x and z)
f2 = not x or not y or not z or w
f3 = (z or w) and y and x
#if f1==1:
#if f2==0:
if f3==1:
print(x,y,w,z)Сравним три полученные таблицы значений с таблицей из условия задачи:

Видим, что для второй функции есть только один возможный набор переменных, причем из него однозначно определяется переменная w = 0, следовательно мы можем определить первый столбец – он соответствует переменной w. Для функций f1 и f3 переменная w = 1, поэтому исключим в получившихся таблицах строки, в которых w = 0. Обратим внимание на третью функцию. Нас интересует строка, в которой содержатся три единицы и один ноль. Этот ноль соответствует переменной z, то есть четвертый столбец определяется однозначно, это переменная z. В таблице для первой функции оставим только те строки, в которых z = 0. Нам подходит только одна строка, в которой два ноля и две единицы. Одна единица соответствует переменной w, вторая – переменной х. То есть можно сделать вывод, что переменной х соответствует третий столбец в заданной таблице, и оставшийся второй соответствует переменной у.
В ответе на задачу записываем wyxz.
Ответ: wyxz

