Некоторые рекомендации о том, как описать проект.
Сегодня обсудим неравномерное кодирование. Ранее рассматривалось равномерное кодирование, при котором каждому значению присваивается двоичный код фиксированной длины. Например, каждый элемент представлен пятью, шестью или восемью битами. Теперь перейдем к ситуации, когда длина кода варьируется: некоторые элементы закодированы коротким числом битов, другие — длинным. Сразу возникает вопрос: почему используется такой подход?
Смысл неравной длины заключается в следующем: разные символы встречаются с неодинаковой частотой. Одни знаки появляются намного чаще, другие гораздо реже. Возьмем, к примеру, русский алфавит.
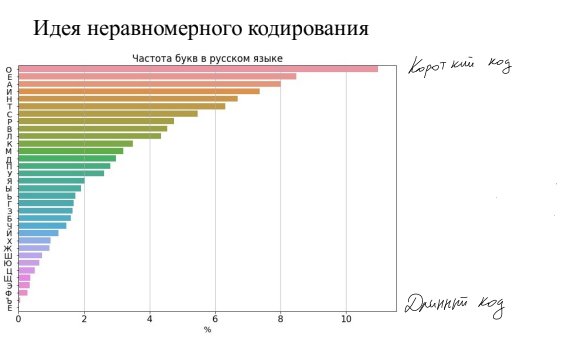
Некоторые буквы («о», «е», «а») используются почти повсеместно, тогда как твердый знак или буква «ё» крайне редки. Отсюда вытекает идея: наиболее распространённые символы можно закодировать меньшим количеством битов, пожертвовав длиной редко встречающихся символов. За счёт такого подхода общий объём данных уменьшается, поскольку суммарная средняя длина всех знаков сокращается.
Это основной принцип работы простейших методов архивации. Часто встречающиеся фрагменты занимают меньше места, редкие — больше, однако общая экономия оказывается значительной благодаря различиям в частотности. Однако стоит учитывать важный нюанс: выбор правильного способа кодировки критичен. Непродуманный подбор приведет к невозможности однозначно восстановить исходное сообщение после сжатия
Суть вопроса заключается в следующем: рассмотрим азбуку Морзе, которая представляет собой первый известный способ двоичного кодирования символов через точки и тире, условно соответствующие нулям и единицам. Здесь важно отметить, что символы имеют различную длину — некоторые состоят всего из одной отметки, другие — из большего числа знаков, вплоть до шести. Такая неравномерность позволяет чаще используемым символам иметь меньшую длину, тогда как редко встречающиеся знаки становятся длиннее.
Однако такая система порождает проблему: отсутствие чёткого разделителя между знаками создаёт риск неоднозначного прочтения сообщений. К примеру, последовательность «точка-тире-точка-точка» можно интерпретировать как одну букву («Л»), две буквы («АИ») или даже три-четыре буквы («ЕТЕЕ»). Неясно, какой вариант верный, ведь отсутствует однозначно определённый порядок чтения.
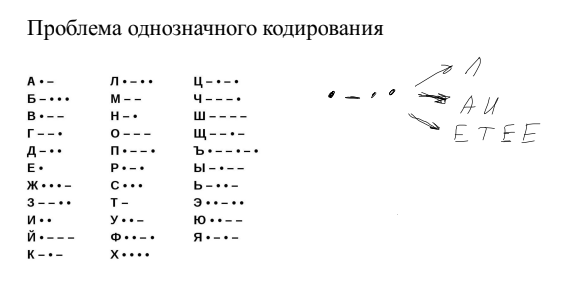
Эта ситуация известна как проблема однозначного кодирования: когда одна запись допускает несколько возможных интерпретаций. Для её решения введено правило, называемое условием Фано, которое гласит: ни одно кодовое слово не должно являться началом другого. Критерий Фано ( ударение падает на первый слог) в области информатики является наиболее часто используемым, хотя и не единственным, правилом.
Примечание Джобса: условие Фано является достаточным, но не необходимым. То есть существуют коды, которые не соответствуют условию Фано, однако являются однозначно декодируемыми.
Этот талантливый человек предложил довольно простое правило однозначного декодирования, которое обеспечивает возможность корректного прочтения любого закодированного таким образом сообщения.
Простота формулировки этой концепции скрывает важное свойство — соблюдение данного условия обеспечивает однозначность расшифровки любого закодированного текста.
Приведём наглядный пример правильной кодировки: предположим, буква «А» обозначается комбинацией «00», буква «Б» — «100», а буква «В» — «101». Эта кодировка корректна именно потому, что никакое из выбранных кодовых слов не выступает началом другого
Кодировка считается корректной, если ни одно кодовое слово не начинается с начала какого-либо другого кодового слова. Рассмотрим пример: пусть заданы три буквы с кодовыми словами АБВ. Если добавить новую букву Г, закодировав её символом «11», то проблем не возникнет, поскольку кодовая комбинация «11» не совпадает с началом любой другой комбинации («А=0», «Б=10», «В=1»).
Однако, если ввести ещё одну букву Д, обозначив её комбинацией «1000», возникает проблема: код «В» становится частью начала кода «Д». Таким образом нарушается принцип однозначности, и появляется риск неоднозначного прочтения последовательности символов. Например, последовательность «1000» теперь можно трактовать двояко: либо как одиночную букву «Д», либо как комбинацию «В+ноль».
Рассмотрим типичную ситуацию экзаменационной задачи формата ЕГЭ. Условие звучит примерно так:
«Имеются пять букв алфавита (АБВГД) с известными кодировками первых четырёх букв. Необходимо подобрать кодовую комбинацию пятой буквы таким образом, чтобы сохранялась однозначность чтения сообщений.»
Для решения этой задачи часто используют визуализацию через построение двоичного дерева.
Представьте графическое изображение дерева, где каждая ветвь делится на два направления:
- Одно направление обозначается цифрой «0»;
- Другое — цифрой «1».
Например, рассмотрим простейший случай, когда первые четыре буквы имеют такие кодировки:
- A = 11
- Б = 01
- В = 100
- Г = 101
- Д = ?
Задача сводится к выбору свободной ветки дерева, которая бы соответствовала условию уникальности каждого начального фрагмента.
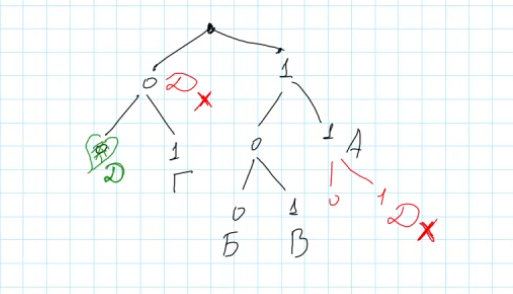
Теперь появляется следующий вопрос: куда правильно поместить букву Д?
Прежде всего важно определить, где точно нельзя размещать новую букву. Запрещено вставлять одну букву сразу после другой. Например, недопустимо расположить букву таким образом: ставить букву Д после А некорректно. Неправильно потому, что тогда буква А окажется частью обозначения буквы Д. Ведь А представлена как “1-1”, а Д как “1-1-1”. Такого допускать нельзя!
Правильное решение — добавлять новые буквы именно в конечные точки схемы, в листья нашего дерева. Листьями называются концы ветвей, заканчивающихся символами. Здесь у нас имеется свободный листок, который пока пустует. Именно туда и можно корректно вписать нашу букву Д. Она не помешает другим буквам и сама не станет началом никакой другой. Таким образом, остаётся лишь одна подходящая позиция для буквы Д, и её кодовая комбинация принимает вид “00”.
Рассмотрим другой пример. Пусть:
А =100,
Б = 01,
В = 00,
Г = 11
Д = ?
Е = ?
Далее добавим сразу две новые буквы. Всего букв шесть, но пока задано лишь четыре.
Теперь возникает задача — подобрать подходящие кодовые комбинации для двух оставшихся символов. Нарисуем графическое представление в виде двоичного дерева.
Начнем ветвление с нулей и единиц: ноль, единица, далее ноль разделяется снова на ноль и единицу. Получаем таким образом узлы В и Б. Следующая веточка даёт последовательность 11 — это соответствует букве Г. Последняя комбинация — 100 — относится к букве A.
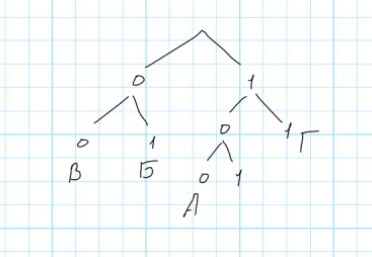
Свободна всего одна позиция, где возможно разместить новое кодовое слово. Однако, нужно закодировать именно две буквы, а не одну.
Очевидно, что необходимо произвести дальнейшее разделение, добавив дополнительный бит. Таким образом, получаем новый уровень, состоящий из двух узлов. Теперь мы можем заполнить оба свободных слота двумя новыми символами. Например, слева ставим букву Д, справа — букву Е. Благодаря этому дополнительному биту мы обеспечили каждой букве уникальное и короткое кодовое обозначение.
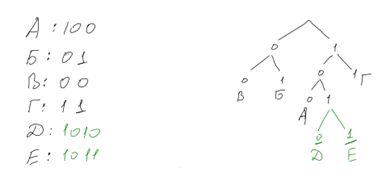
Важно отметить, что в текущей постановке задачи выбор расположения букв Д и Е совершенно неважен и никак не влияет на результат.
Задача № 1 (6699)
По каналу связи передаются сообщения, содержащие только пять букв: А, Б, В, Г, Д. Для передачи используется неравномерный двоичный код, удовлетворяющий условию Фано. Для букв А, Б, В и Г используются кодовые слова 001, 010, 101, 11 соответственно. Укажите кратчайшее кодовое слово для буквы Д, при котором код будет допускать однозначное декодирование.
Если таких кодов несколько, укажите код с наибольшим числовым значением.
Решение
Для решения построим бинарное дерево кодирования. Получаем ветвление на две стороны: слева направо идут значения 0 и 1. Следуя этому принципу, начертим путь каждого из известных кодовых значений:
- 11 — это буква Г,
- 101 — буква В,
- 001 — буква А,
- 010 — буква Б.
Таким образом, изобразив дерево, видим свободные узлы длиной три бита, доступные для размещения буквы Д. Из них нужно выбрать оптимальное решение согласно заданному условию.
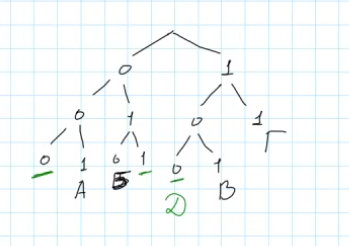
Поскольку коды одинаковой длины, выбираем позицию, соответствующую самому большому числу среди трёхбитных комбинаций: 000, 011 и 100. Наибольшее значение среди них очевидно — это комбинация 100. Следовательно, букве Д целесообразно назначить именно её.
Ответ: 100
Задача №2 (1701)
Для кодирования некоторой последовательности, состоящей из букв А, Б, В, Г, Д, Е, Ж, З, И, Й. решили использовать неравномерный двоичный код, удовлетворяющий условию Фано. Для букв А, Б, В, Г, Д, Е, Ж, З, И использовали соответственно кодовые слова 00, 111, 1000, 1001, 1010, 1100, 1101, 010, 011. Укажите кратчайшее возможное кодовое слово для буквы Й, при котором код будет допускать однозначное декодирование. Если таких кодов несколько, укажите код с наименьшим числовым значением.
Решение
Для решения данной задачи воспользуемся графическим методом построения дерева префиксного кода. Из условия известно, что первые девять букв уже имеют заданные коды, и теперь нужно найти оптимальный код для буквы Й.
Нарисуем бинарное дерево следующим образом:
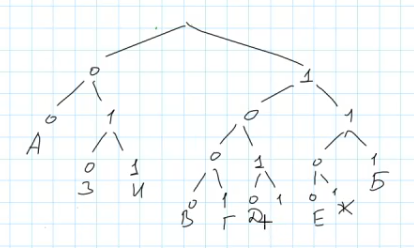
Теперь проверяем наличие свободных ветвей, подходящих для добавления нового символа Й. Согласно построенному дереву видим единственное свободное место после цифры 1 слева от корня.
Итак, оптимальная длина кода для буквы Й равна четырём битам, что является минимальной длиной среди возможных комбинаций, обеспечивающих корректное восстановление последовательности символов.
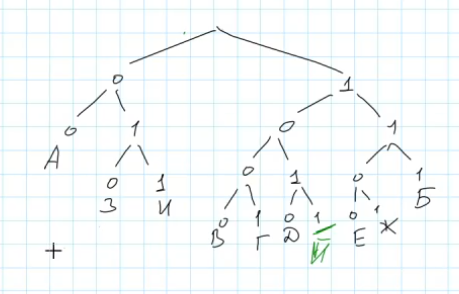
Ответ: 1101
Задача № 3 (6701)
По каналу связи передаются сообщения, содержащие только восемь букв: А, Б, В, Г, Д, Е, Ж, З. Для передачи используется неравномерный двоичный код, удовлетворяющий условию Фано. Для некоторых букв кодовые слова известны: В – 00, Г – 1000, Д – 111, Е – 1001, Ж – 01, 3 – 110. Какое наименьшее количество двоичных знаков потребуется для кодирования двух оставшихся букв? В ответе запишите суммарную длину кодовых слов для букв А и Б.
Решение
Начнем строить дерево кодов:
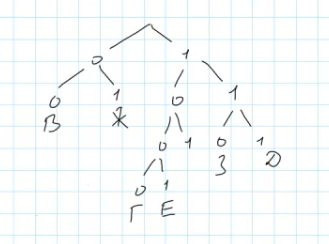
На рисунке видно, какие пути заняты известными кодовыми словами. Осталось найти свободные пути минимальной длины для букв А и Б. Мы видим одну свободную ветку, куда можем добавить еще одно разветвление, обеспечив дополнительное свободное пространство для наших букв.
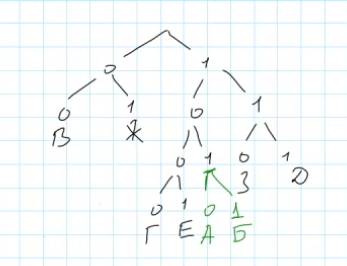
Тогда коды будут такими:
- A=1010
- B=1011
Тогда сумма длин кодов составит 4 + 4 = 8. Именно эта величина является правильным решением данной задачи.
Ответ: 8
Задача № 4 (1711)
По каналу связи передаются сообщения, содержащие только семь букв: А, Б, В, Г, Д, Е и Ж. Для передачи используется двоичный код, удовлетворяющий условию Фано. Для буквы А используется кодовое слово 1; для буквы Б используется кодовое слово 01. Какова минимальная общая длина кодовых слов для всех семи букв?
Решение
Начнём построение двоичного дерева кодирования. Известно, что буква А кодируется одним символом «1», а буква Б — двумя символами «01».
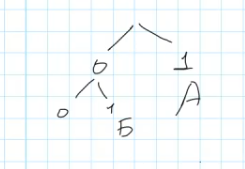
Нам осталось закодировать ещё пять букв (В, Г, Д, Е, Ж). Изобразим дерево следующим образом:
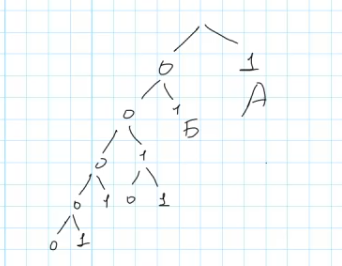
Теперь распределим оставшиеся буквы («В», «Г», «Д», «Е», «Ж») по оставшимся свободным узлам дерева:
- В: путь «000»
- Г: путь «0010»
- Д: путь «00110»
- Е: путь «00111»
- Ж: путь «001110» (можно было бы выбрать другой узел, но длина будет одинаковой).
Посчитаем длины всех полученных кодов и просуммируем их.
| Буква | Кодовое слово | Длина |
| А | 1 | 1 |
| Б | 01 | 2 |
| В | 000 | 3 |
| Г | 0010 | 4 |
| Д | 00110 | 5 |
| Е | 00111 | 5 |
| Ж | 001110 | 6 |
Ответ: 25
Задача №5 (6435)
Все заглавные буквы русского алфавита закодированы неравномерным двоичным кодом, в котором никакое кодовое слово не является началом другого кодового слова. Это условие обеспечивает возможность однозначной расшифровки закодированных сообщений. Кодовые слова для некоторых букв известны: А – 000, Б – 01, В – 100, Г – 11, Д – 001. Укажите возможный код минимальной длины для буквы Я. Если таких кодов несколько, укажите тот из них, который имеет минимальное числовое значение.
Решение
Здесь кроется ловушка. Если ранее задания содержали строгие рамки, скажем, было указано конкретное количество символов («семь букв» или «восемь»), то теперь речь идёт обо всех прописных буквах русской азбуки, которых ровно тридцать три. Разумеется, кодировать каждую букву вручную вовсе необязательно, однако учитывать этот факт крайне важно.
Построим бинарное дерево кодирования:
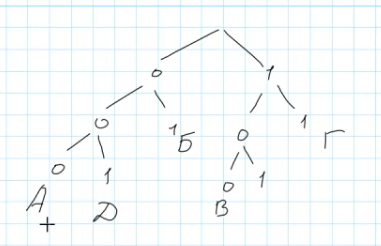
Теперь нам предстоит выбрать оптимальный путь для буквы «Я». Сразу отметим свободную позицию 101 рядом с буквой «В»
Однако такой подход неверен, поскольку дальнейшее расширение дерева становится невозможным, и разместить оставшиеся буквы будет негде.
Следовательно, единственно верным решением будет пойти глубже по дереву, создав новые ветви от корня
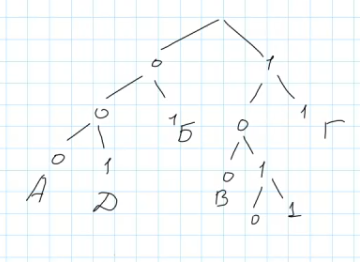
Получив таким образом две новых ветви, на одну из них мы помести букву Я, а вторая ветвь может быть использована для всех прочих букв алфавита, причем, нам уже не важно, как они будут располагаться.
В задаче требуется указать код минимально возможной длины и имеющий минимальное числовое значение, соответственно это будет код 1010.
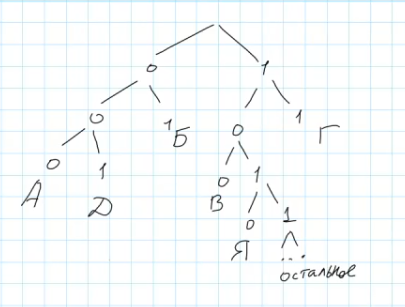
Ответ: 1010
Задание №6 (8157)
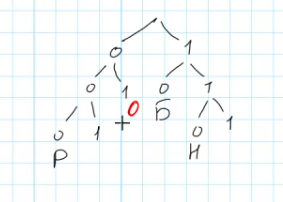
По каналу связи передаются сообщения, содержащие только буквы из набора: Б, К, Р, О, Н. Для передачи используется двоичный код, удовлетворяющий условию Фано. Кодовые слова для некоторых букв известные Б – 10, Н – 110, Р – 000. Для двух оставшихся букв К и О кодовые слова неизвестны. Какое количество двоичных знаков требуется для кодирования слова КОРОБОК, если известно, что оно закодировано минимально возможным количеством двоичных знаков?
Решение
Для решения данной задачи рассмотрим следующее: нам необходимо выбрать наиболее эффективные коды для букв К и О таким образом, чтобы итоговая длина слова была минимальной.
Анализируем исходное слово «коробок»:
- О -3
- К -2
- Б – 1
- Р — 1
Поскольку буква О повторяется наибольшее число раз, её код должен быть коротким, иначе суммарная длина существенно увеличится.
Исходя из известных кодов, построим возможное дерево:
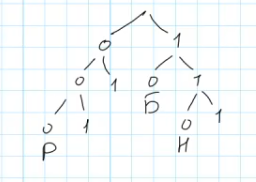
Теперь остаётся закодировать буквы К и О.
Так как буква О в заданном слове встречается чаще других букв (3 раза) присвоим ей самый возможно короткий код длиной состоящий из 2 символов
О – 01
Буква К может располагаться на любой из двух оставшихся возможных позиций, в любом случае длина её кода будет равняться трем.
Подставив значения длин кодов в слово, просуммируем общее количество знаков
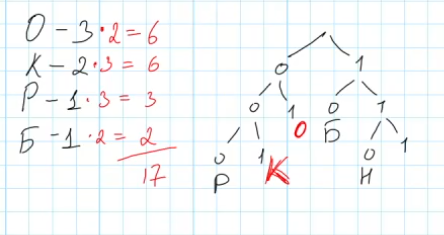
Ответ: 17
Задание № 7(7914)
По каналу связи передаются сообщения, содержащие только семь букв: Е, И, М, Т, О, Р, Я. Для передачи используется двоичный код, удовлетворяющий условию Фано. Это условие обеспечивает возможность однозначной расшифровки закодированных сообщений. Кодовые слова для некоторых букв известны: Е – 01, И – 001, О – 0001, Я –101. Для трёх оставшихся букв Т, Р и М кодовые слова неизвестны. Какое наименьшее количество двоичных знаков требуется для кодирования слова ТЕРРИТОРИЯ?
Решение
Посчитаем частоту каждой буквы в слове:
- Т: 2,
- Р: 3,
- И: 2,
- Е: 1,
- О: 1,
- Я: 1.
Из условия известно, что буквы Т, Р и М требуют дополнительного кодирования. При этом Буква Т встречается дважды, Р трижды, а буквы М в этом слове нет, следовательно Самый короткий из возможных кодом мы должны постараться присвоить букве Р, следом разместить букву Т, длина кода для буквы М может быть любой.
Начнём построение дерева, при этом мы разветвляем дерево только там, где у нас размещаются буквы с известными кодами.
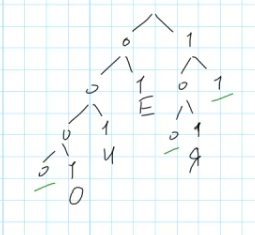
Видим, что у нас есть три места, куда мы можем поставить буквы. Теперь добавим остальные буквы согласно принципу минимальной длины для наиболее используемых символов:
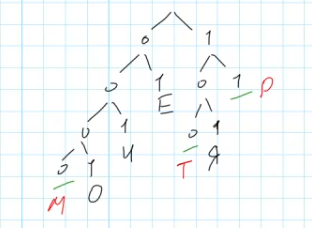
Теперь считаем суммарную длину кодового слова

Ответ: 27
Задание №8 (6883 OpenFIPI) бонус
По каналу связи передаются сообщения, содержащие только буквы из набора: А, З, К, Н, Т. Для передачи используется двоичный код, удовлетворяющий условию Фано. Это условие обеспечивает возможность однозначной расшифровки закодированных сообщений. Кодовые слова для некоторых букв известны: К – 1, Н – 001. Для трёх оставшихся букв А, З и Т кодовые слова неизвестны. Какое количество двоичных знаков потребуется для кодирования слова КАНТАТА, если известно, что оно закодировано минимально возможным количеством двоичных знаков?
Решение
Посчитаем частоту каждой буквы в слове:
- А: 3,
- Т: 2,
- Н: 1,
- К: 1,
Обратим внимание, что в слове «КАНТАТА» нет буквы «З». Таким образом, задача сводится к оптимальному выбору кодов для букв «А» и «Т», чтобы минимизировать суммарную длину всего слова. Рассмотрим возможные варианты распределения кодовых ветвей:

Видим, что у нас есть два места и надо закодировать три буквы. Рассмотрим возможные варианты распределения кодовых ветвей. Предположим, мы раздваиваем ветвь нуля («0»). Получаем следующую структуру:

Тогда имеем:
- K=1 ( 1 знак);
- Н=001 ( 3 знака);
- A=01 ( 2 знака);
- Оставшиеся буквы «T» и «З» будут иметь длинные ветви длиной 4 .
Посчитаем общее число битов для слова «КАНТАТА»:
- K встречается один раз: 1×1=1 ;
- A встречается трижды: 3×2=6 ;
- T встречается дважды: 2×4=8 ;
- Н встречается единожды: 1×3=3 .
Итого получаем: 1+6+8+3=18 битов.
Рассмотрим второй случай. Раздваиваем ветвь единицы («1»), получив одинаковые по длине ветки

Здесь каждая новая буква получает собственный путь равной длины (по 3 бита)
Посчитаем снова:
- K один раз: 1×1=1 ;
- A трижды: 3×3=9 ;
- T дважды: 2×3=6 ;
- Н одна: 1×3=3 .
Суммируем: 1+9+6+3=19 битов.
Сравнив оба подхода, видим, что первый оказался более оптимальным, поскольку привел к меньшему количеству битов. Во втором случае итоговая сумма превышает первое значение. Таким образом, из этих двух вариантов выгоднее первый вариант с итоговой суммой 18.

Ответ: 18
Задание №8(4823)
Все заглавные буквы русского алфавита закодированы неравномерным двоичным кодом, для которого выполняется условие Фано: никакое кодовое слово не совпадает с началом другого кодового слова. Известно, что слову ТРОПОТ соответствует код 001110110001001. Какой код соответствует слову ПОРТ?
Решение
Начнём с анализа шифровки слова «ТРОПОТ»: оно состоит из шести букв, причём начальная и конечная буквы совпадают («Т»). Отсюда ясно, что оба раза используется одна и та же последовательность символов, соответствующая букве «Т».
Предположительно:
- Код буквы «Т» — три символа: 001.

Следующая буква после первой «Т» — «Р», далее — «О». Рассмотрим фрагмент исходного кода от второго до четвёртого символа включительно (111). Попробуем предположить следующее распределение:
- Буква «Р» обозначается двумя цифрами: 11,
- Затем идёт буква «О», которую обозначаем символом 0.
Далее идёт вторая буква «П», её пока обозначим условно как неизвестный код. Следующие символы (10) предположительно соответствуют букве «О». Теперь рассмотрим оставшуюся часть последовательности:
- После повторяющейся пары «ТО» снова идут символы 001, что подтверждает предположение о тройственном кодировании буквы «Т».
Проверяем правильность наших предположений путём построения дерева возможных вариантов.

Проверяя структуру построенного нами бинарного дерева, убеждаемся, что выбранные нами соответствия соблюдают правило Фано:
- Т = 001,
- О = 01,
- Р = 11,
- П = 100.
Таким образом, теперь можем записать требуемый код для слова «ПОРТ»:
Таким образом, теперь можем записать требуемый код для слова «ПОРТ»:
- П → 100
- О → 01
- Р → 11
- Т → 001
Итоговый код для слова «ПОРТ»:
1000111001 .

Ответ: 1000111001
Задание №9(1237 Статград)
Все заглавные буквы русского алфавита закодированы неравномерным двоичным кодом, в котором никакое кодовое слово не является началом другого кодового слова. Это условие обеспечивает возможность однозначной расшифровки закодированных сообщений.
Известно, что все кодовые слова содержат не меньше двух двоичных знаков, а слову БАРАН соответствует код 10011111011010. Какое наименьшее количество двоичных знаков может содержать сообщение, кодирующее слово РОБОТ?
Решение
Предположим, что первая последовательность 100 — это буква Б, вторая 111 — буква Р, третья 110 — буква А, четвертая снова 110 — тоже буква А, пятая 10 — буква Н.

Проверяем правильность выбора фрагментов через построение дерева кодирования:
Дерево выглядит следующим образом:

Теперь перейдем к кодированию слова РОБОТ. Учитывая, что в условии задачи указано, что закодированы все заглавные буквы русского алфавита , такой вариант расположения букв нас не устроит:

Тогда разместив букву О на минимальной позиции, мы далее разветвим оставшуюся веточку:

Таким образом мы закодировали все буквы слова РОБОТ и имеем место под буквы невостребованные, но указанные в задании. Таким образом мы можем прописать коды всех букв в слове робот и вычислить их суммарную длину.

Ответ: 13
Задание №10 (3503)
По каналу связи передаются сообщения, содержащие только шесть букв: Т, Е, Н, С, И, В. Для передачи используется двоичный код, допускающий однозначное декодирование. Кодовые слова для букв известны: Т – 010, Е – 0100, Н – 1100, С – 01000, И – 0110, В – 1110. Как можно сократить код для буквы Н, чтобы сохранялось свойство однозначности декодирования? Если таких кодов несколько, в качестве ответа указать код наименьшей длины.
Решение
Для решения подобных задач используется Обратное условие Фано:

Читаем, или переворачиваем слова в обратную сторону.

Прочитав слова наоброт, дальше мы действуем по установленному алгоритму,т.е. рисуем бинарное дерево:

Т.е. нам нужно подобрать более короткий код для буквы Н. Очевидно, что его расположение будет следующим:

Ответ : 1
В общем случае решения подобных задач, необходимо кода перевернуть обратно.
🤖 Пример задания на распознавание кода внутри слова
Все заглавные буквы русского алфавита закодированы неравномерным двоичным кодом, в котором никакое кодовое слово не является началом другого кодового слова. Это условие обеспечивает возможность однозначной расшифровки закодированных сообщений. Известно, что слову КАША соответствует код 011011010. Какое наименьшее количество двоичных знаков может содержать сообщение, кодирующее слово ОСОКА?
💌 Решение
- Начнем расшифровку кодового слова с конца. “0” не может соответствовать букве “А”, потому что в начале последовательности есть “0”, входящий в кодовое слово для буквы “К” – иначе условие Фано не будет соблюдено.
- Кодовое слово “10” вполне может подойти! Кодовые слова “010” и “1010” не подходят, так как встречаются в последовательности единожды, а буква “А” – дважды.
- Если кодовое слово будет длиннее, не получится закодировать остальные. Тогда, перебирая различные варианты, приходим к выводу, что единственное распределение, при котором слово кодируется,а код соответствует условию Фано – К — 01, А — 10, Ш — 110.
- Используя удобный метод кодирования букв и учитывая правило Фано, сделаем вывод, что для букв “О” и “С” могут подойти кодовые слова “00” и “1110”.
- Так как “О” встречается дважды, для неё выберем кодовое слово короче, тогда длина кодового слова для комбинации букв “ОСОКА” будет составлять 2+4+2+2+2 = 12 символов.
- Ответ: 12



