ФИПИ заявляет восьмое задание в ЕГЭ как задачу на проверку знания основ комбинаторного счета, и, несмотря на то, что последние годы задачу №8 практически невозможно решить аналитически, применяя комбинаторику, основы её важно знать, так как это поможет в подготовке и при решении других задач, а также в целом в математике и информатике. Важно освоить базовые действия комбинаторного счета, чтобы иметь надежную базу и не попасть в сложную ситуацию на экзамене.
Основные правила комбинаторики — правила суммы и произведения.
Правило суммы: если действие А можно выполнить N способами, а действие B — M способами, и выбирать между ними можно только одно, то всего способов выполнить либо А, либо В — N + M. Например, у вас есть 5 рубашек и 3 футболки. Тогда, выбирая одежду на день, у вас 8 способов: одну из рубашек или одну из футболок, при этом нельзя комбинировать их одновременно.
Правило произведения применимо, когда нужно выполнить последовательность действий: если действие А можно сделать M способами, а после этого — действие В, которое можно выполнить N способами, то всего вариантов — M * N. Например, в ресторане 4 варианта первого блюда и 6 — второго, тогда всего 4 * 6 = 24 комбинации.
Это правило работает для любых последовательных выборов. Оно называется также правилом всевозможных комбинаций или декартовым произведением — описывает все возможные пары элементов из двух множеств.
Задача № 1
Сколько слов длины 5, начинающихся с гласной буквы, можно составить из букв М, Е, C, Я, Ц? Каждая буква может входить в слово несколько раз. Слова не обязательно должны быть осмысленными словами русского языка.
Решение
Нарисуем схему кодового слова. Всего в слове 5 букв:

Известно, что на первой позиции могут быть только гласные буквы (Е или Я), то есть на этой позиции может быть одна из двух букв, её можно заполнить двумя разными способами. На остальных 4 позициях может быть любая буква из набора М, Е, C, Я, Ц, то есть каждую из остальных позиций можно заполнить пятью разными способами:
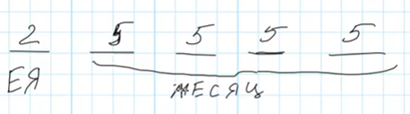
Для того, чтобы посчитать общее количество возможных комбинаций, то есть кодовых слов, применим правило произведения – перемножим число вариантов для каждой позиции:
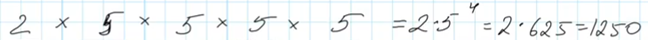
Получили, что из набора М, Е, C, Я, Ц, можно получить 1250 пятибуквенных кодовых слов, если первая буква может быть только гласной.
Ответ: 1250
Задача №2
Сколько слов длины 6, начинающихся с гласной буквы и заканчивающихся согласной буквой, можно составить из букв К, А, Ш? Каждая буква может входить в слово несколько раз. Слова не обязательно должны быть осмысленными словами русского языка.
Решение
Нарисуем схему кодового слова. Всего в слове 6 букв:

Известно, что на первой позиции может быть только гласная буква (А), то есть эта позиция может быть заполнена только одним способом. На средних 4 позициях может быть любая буква из набора К, А, Ш, то есть каждую из второй – пятой позиций можно заполнить тремя разными способами. На последней позиции могут быть только согласные буквы (К или Ш), то есть на этой позиции может быть одна из двух букв, её можно заполнить двумя разными способами:
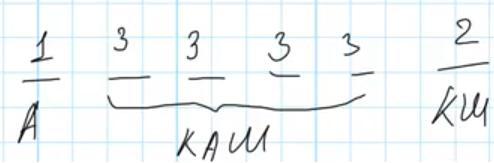
Для того, чтобы посчитать общее количество возможных комбинаций, то есть кодовых слов, применим правило произведения – перемножим число вариантов для каждой позиции:

Получили, что из набора К, А, Ш можно получить 162 шестибуквенных кодовых слов, если первая буква может быть только гласной, а последняя только согласной.
Ответ: 162
Задача № 3
Игорь составляет слова из букв Д, O, Т, А. Слово может иметь длину от 3 до 5 букв. Сколько слов может составить Игорь?
Решение
Игорь составляет слова с различным количеством букв – 3, 4 или 5. Каждое слово состоит из букв Д, O, Т, А в разных сочетаниях без ограничений, то есть на каждой позиции каждого слова может стоять любая из 4 букв. Нарисуем схемы всех слов:
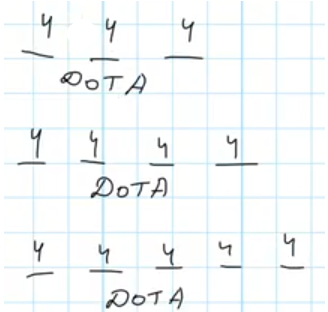
Чтобы подсчитать общее количество слов, которые сможет составить Игорь, нужно сложить количество возможных комбинаций для каждого из слов, а количество комбинаций для каждого слова посчитать по правилу произведения, перемножив количество вариантов заполнения каждой позиции слова.
Получили, что Игорь сможет составить 1344 кодовых 3-5 буквенных слова из набора Д, О, Т, А.
Ответ: 1344
Размещение
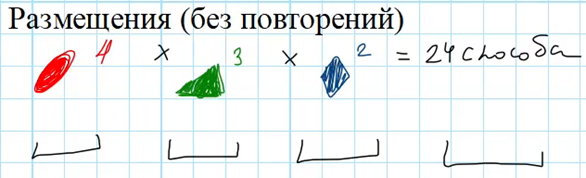
Размещение — это распространённая ситуация, когда нужно разместить несколько фигур в различных местах. Например, у нас есть 4 коробки и один красный мячик – в этом случае есть 4 способа его разместить – можно положить в любую из 4х коробок. Если добавить к красному мячику зеленый треугольник, то для него остаётся 3 варианта — можно разместить его в любой свободную коробку, кроме той, куда уже положили мячик. Если добавить к красному мячику и зеленому треугольнику синий ромбик, то для него остаётся только 2 варианта — можно разместить его в любую оставшуюся свободную коробку, кроме тех, куда уже положили мячик и треугольник. Таким образом, для каждого следующего предмета количество способов размещения уменьшается, так как свободных коробок становится меньше. В итоге, чтобы найти общее число вариантов размещения всех фигур, нужно последовательно выбрать место для каждого и перемножить количество вариантов. Например, при размещении трех фигур — получится 4 * 3 * 2 = 24 варианта:
Задача № 4
Вася составляет 6-буквенные слова, в которых есть только буквы Б, У, Л, К, А, причём буква У используется в каждом слове ровно 1 раз. Каждая из других допустимых букв может встречаться в слове любое количество раз или не встречаться совсем. Словом считается любая допустимая последовательность букв, не обязательно осмысленная. Сколько существует таких слов, которые может написать Вася?
Решение
Нарисуем схемы возможных шестибуквенных слов. Буква У должна встречаться ровно один раз, то есть возможно 6 вариантов схемы:
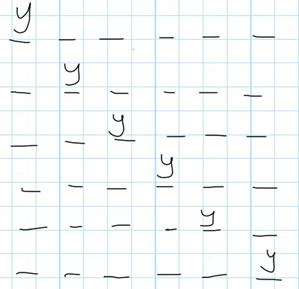
На пяти остальных позициях может встретиться любая из четырех оставшихся из набора букв (Б, Л, К, А), потому что букву У мы уже разместили. То есть каждая из схем имеет 4*4*4*4*4 = 1024 варианта слов:
Всего у нас 6 возможных схем слов, 6*1024 = 6144.
Вася может составить 6144 различных кодовых слова.
Ответ: 6144
Задача №5
Ученица составляет 5-буквенные слова из букв ЖИРАФ. При этом в каждом слове ровно одна буква Ж, слово не может начинаться на букву Ф и заканчиваться буквой Р. Какое количество слов может составить ученица?
Решение
Нужно рассмотреть 5 различных вариантов схем слова, поскольку известно, что в каждом слове содержится ровно одна буква Ж – она может стоять на одной из 5 позиций:
Букву Ж мы разместили, у нас осталось для размещения 4 букв (И, Р, А, Ф). Ограничения есть только для первой и последней буквы в слове, поэтому на позициях внутри слова может стоять любая из 4 букв. На первой позиции не может находиться буква Ф, а на последней – буква Р. Поэтому для тех слов, которые на начинаются и не заканчиваются буквой Ж, возможны три варианта заполнения первой и последней позиции:
Количество комбинаций – это произведение всех возможностей, для каждой схемы посчитаем отдельно с помощью IDLE.

Общее количество комбинаций равно 2*192 + 3*144 = 816.
Ученица может составить 816 слов.
Ответ: 816
Перестановки.
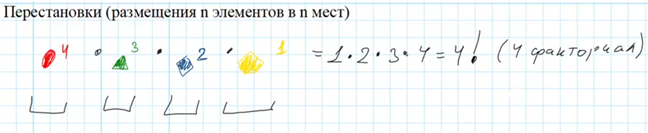
Перестановки — это размещение n элементов в n мест. Например, у нас есть 4 коробки и 4 фигуры: один красный мячик – в этом случае есть 4 способа его разместить – можно положить в любую из 4х коробок, один зеленый треугольник – его можно разместить его в любой свободную коробку, кроме той, куда уже положили мячик (3 варианта размещения), один синий ромбик, который можно разместить его в любую из двух оставшихся свободных коробок (2 варианта размещения) и один желтый пятиугольник – его можно разместить единственным способом. В итоге, чтобы найти общее число вариантов размещения всех фигур, нужно последовательно выбрать место для каждого и перемножить количество вариантов. Например, при размещении четырех фигур — получится 1*2*3*4 = 24 варианта. Операция перемножения последовательно чисел от единицы до какого-то числа включительно называется факториалом этого числа, пишут 4! = 1*2*3*4=24.
Размещения с повторением (сочетания)
Сочетание – это чрезвычайно важная операция в комбинаторике, размещение нескольких одинаковых предметов. В отличие от перестановок, мы имеет дело не с различными предметами, а с одинаковыми. То есть, например, мы имеем четыре коробки и два одинаковых синих мячика. Если бы они были различными, то можно было бы сказать, что первый синий мячик можно разместить 4 способами, а для второго останется 3 варианта размещения, и общее количество возможностей разместить два синих мячика в четырех коробках равно 12.
Но два синих мячика одинаковы, поэтому на самом деле возможны только 6 различных вариантов, остальные будут их дублировать:
Поэтому количество вариантов размещений двух одинаковых предметов в четырех местах подсчитывается так:
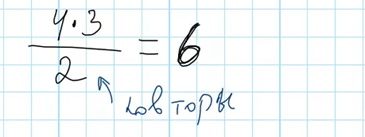
Теперь разберем ситуацию, в которой у нас есть 3 одинаковых зеленых кубика и 5 мест для размещения. Если бы кубики были различны, то первый можно было бы разместить 5 способами, второй – 4, и третий тремя. Но кубики одинаковы, и размещения дублируются. Рассмотрим пример – разместим кубики в первое, третье и четвертое место для хранения. Технически это можно сделать шестью различными способами – способы видны на примере, кубика присвоены номера.
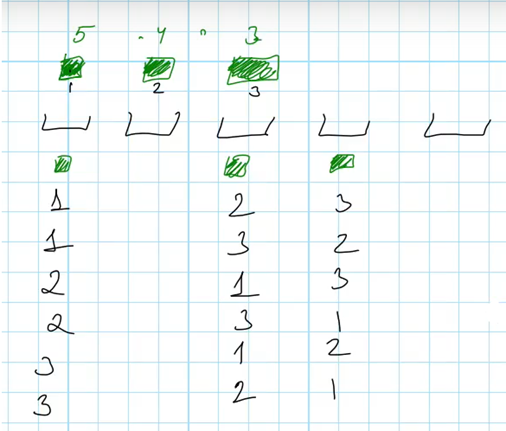
Но физически все шесть способов одинаковы, из пяти мест для размещения заняты три – первое, третье и четвертое. То есть, что бы убрать дубликаты, нужно количество размещений поделить на количество перестановок:
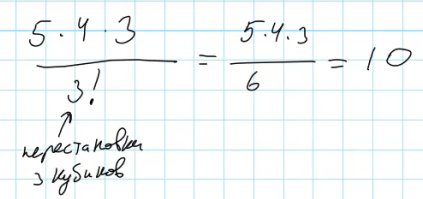
Сочетания обозначаются следующим образом:
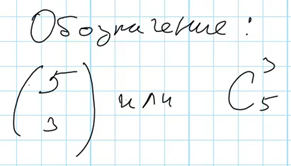
Задание №6
Вася составляет 6-буквенные слова, в которых есть только буквы К, А, Н, Т, причём буква К используется в каждом слове ровно 2 раза. Каждая из других допустимых букв может встречаться в слове любое количество раз или не встречаться совсем. Словом считается
любая допустимая последовательность букв, не обязательно осмысленная. Сколько существует таких слов, которые может написать Вася?
Решение
Нарисуем схему кодового слова. Всего в слове 6 букв, причем буква К используется ровно 2 раза в каждом слове. В это задаче удобнее посчитать через сочетание. В каждом слове должно встречаться 2 буквы К, количество способов, которым можно разместить две буквы вычислим как 6 *5 / 2 = 15. То есть существует 15 способов разместить две буквы К в слове.
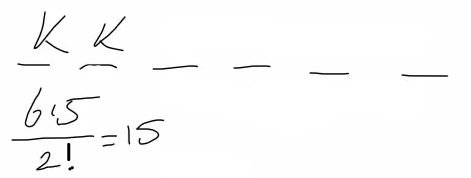
На остальных четырех позициях в слове может стоять любая из трех оставшихся букв набора (А, Н, Т):
Количество комбинаций – это произведение всех возможностей, то есть 15*3*3*3*3 = 15*34 = 15*81 = 1215:

Вася может написать 1215 различных кодовых слова.
Ответ: 1215
Задание № 7
Иван составляет 5-буквенные слова из букв А, Б, В, Г, Д, Я. В каждом слове содержится ровно три буквы Я. Сколько различных кодовых слов может составить Иван?
Решение
Нарисуем схему кодового слова. Всего в слове 5 букв, причем буква Я используется ровно 3 раза в каждом слове. В это задаче удобнее посчитать через сочетание. В каждом слове должно встречаться 3 буквы Я, количество способов, которым можно разместить три буквы вычислим как 5*4*3/ 3! = 10. То есть существует 10 способов разместить три буквы Я в пятибуквенном слове.
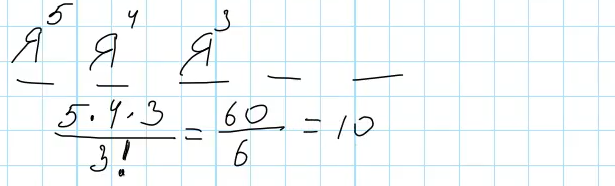
На остальных двух позициях в слове может стоять любая из пяти оставшихся букв набора (А, Б, В, Г, Д):

Количество комбинаций – это произведение всех возможностей, то есть 10*5*5 = 10*25 = 250.
Иван может написать 250 различных кодовых слов.
Ответ: 250
Задание №8
Вася составляет 4-буквенные слова, в которых есть только буквы Л, Е, Т, О, причём буква Е
используется в каждом слове 2 или 3 раза. Каждая из других допустимых букв может встречаться в слове любое количество раз или не встречаться совсем. Словом считается любая допустимая последовательность букв, не обязательно осмысленная. Сколько существует таких слов, которые может написать Вася?
Решение
Рассмотрим два варианта схем слов отдельно, подсчитаем количество вариантов для каждой схемы, а потом сложим для получения ответа на задачу.
Рассмотрим схему слов, в которых встречается ровно две буквы Е. Количество возможных способов разместить ровно две буквы Е в слове из 4 букв считаем как количество сочетаний из 4 по 2. Оно равно шести. На оставшихся двух позициях в слове может быт размещена любая из трех букв Л, Т, О. Общее количество слов, в которых встречаются ровно 2 буквы Е, равно 6*3*3 = 54.

Рассмотрим схему слов с тремся буквами Е. Количество возможных способов разместить ровно три буквы Е в слове из 4 букв считаем как количество сочетаний из 4 по 3. Оно равно четырем. На оставшейся позиции в слове может быт размещена любая из трех букв Л, Т, О. Общее количество слов, в которых встречаются ровно три буквы Е, равно 4*3 = 12.

Всего Вася сможет написать 54 + 12 = 66 слов.
Ответ: 66
Задание №9
Определите количество пятизначных чисел, записанных в пятеричной системе счисления, которые не начинаются с нечетных цифр, не оканчиваются цифрами 1 или 4, а также содержат в своей записи не более одной цифры 3.
Решение
Пятеричная система исчисления состоит из 5 цифр – 0, 1, 2, 3, 4. При этом число не может начинаться на 0. Нарисуем схемы возможных пятизначных чисел, учитывая ограничения. Для начала учтем, что цифра 3 должна встречаться в записи не более одного раза – то есть одна может либо не встречаться вообще, либо встретиться ровно один раз. Рассмотрим первый вариант – в числе не встречается цифра 3: число не может начинаться с нечетной цифры и нуля, следовательно, на первой позиции могут стоять цифры 2 или 4 (всего два варианта), на средних позициях могут встречаться цифры 0, 1, 2, 4 – всего четыре варианта для каждой из трех средних позиций, число не может оканчиваться цифрами 1 и 4, следовательно, на пятой позиции могут находиться только числа 0 и 2, всего два варианта. Количество возможных чисел без тройки в записи найдем по правилу перемножения 2*4*4*4*2 = 256:

Рассмотрим варианты, при которых в записи числа встречается ровно одна цифра 3, при этом она не может стоять на первой позиции, так как число не может начинаться с нечетной цифры. Получается, у нас возможны 4 различных схем записи чисел, красная цифра 3 на схеме означает именно запись цифры, но не количество вариантов цифр. Для других позиций в числах действуют те же ограничения, что и для записи схемы чисел без тройки.

Количество возможных чисел с одной тройкой в записи для каждой схемы найдем по правилу перемножения.
Посчитаем общее количество вариантов чисел с помощью IDLE:

Количество пятизначных чисел, записанных в пятеричной системе счисления, которые не начинаются с нечетных цифр, не оканчиваются цифрами 1 или 4, а также содержат в своей записи не более одной цифры 3, равно 576.
Ответ: 576
Задание №10
Петя составляет пятибуквенные слова перестановкой букв слова МАСКА. Сколько всего различных слов может составить Петя?
Решение
Речь в задаче идет о перестановках, то есть набор букв в словах всегда одинаковый, меняется только их позиция в слове. Если бы все буквы в наборе из 5 букв были различны, то количество перестановок (количество возможных пятибуквенных слов) можно было бы вычислить как 5!:

Но в задаче указано, что в наборе есть две повторяющиеся буквы А. В этом случае часть из слов будут дублировать друг друга. Поэтому, чтобы получить количество различных слов, которые может получить Петя, нужно количество всех перестановок поделить на 2!:

Петя сможет составить 60 различных слов.
Ответ: 60
Задание №11
Петя составляет пятибуквенные слова перестановкой букв слова МАРГАРИТА. Сколько всего различных слов может составить Петя?
Решение
Речь в задаче идет о перестановках, то есть набор букв в словах всегда одинаковый, меняется только их позиция в слове. Если бы все буквы в наборе из 9 букв были различны, то количество перестановок (количество возможных пятибуквенных слов) можно было бы вычислить как 9!:

Но в наборе есть три повторяющиеся буквы А и две повторяющиеся буквы Р. В этом случае часть из слов будут дублировать друг друга. Поэтому, чтобы получить количество различных слов, которые может получить Петя, нужно количество всех перестановок поделить на 3! и на 2!:

Считаем с помощью IDLE. Петя сможет составить 30240 различных слов.
Ответ: 30240
Задание №12
Петя составляет 5-буквенные слова из букв К, Л, О, У, Н. Каждую букву нужно использовать ровно 1 раз, при этом нельзя ставить подряд две гласные или две согласные. Сколько различных кодов может составить Петя?
Решение
В наборе букв К, Л, О, У, Н есть три согласных буквы – К, Л, Н, и две гласных буквы – О, У. Поскольку нельзя ставить подряд две гласные или две согласные, возможен единственный вариант расположения букв в слове:
 ,
,
Где С – согласная буква, Г – гласная.
Так как речь идет о перестановках, каждую букву можно использовать только один раз, то получается, что для первой позиции возможны 3 варианта букв (любая из согласных), для второй – два варианта букв (любая из гласных), для третей — два варианта букв (любая из двух оставшихся согласных), для четвертой и пятой позиции возможет только один вариант – оставшиеся гласная и согласная буквы, соответственно.

Применим правило произведения – перемножим число вариантов для каждой позиции, получим, что Петя может составить 12 различных кодов.
Ответ: 12
Задача №13
Определите количество трёхзначных чисел, записанных в десятичной системе счисления, в записи которых ровно одна цифра 8, при этом чётные и нечётные цифры чередуются.
Решение
Десятеричная система исчисления состоит из 10 цифр – 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. При этом число не может начинаться на 0. Нарисуем схемы возможных трехзначных чисел, учитывая ограничения. Для начала учтем, что цифра 8 должна встречаться в записи ровно один раз, то есть, у нас возможны три варианта записи чисел:

Четные цифры – 0,2,4,6,8, при этом будем учитывать, что 8 уже использована, а 0 не может стоять на первой позиции.
Нечетные цифры – 1,3,5,7,9.
Учитывая, что чётные и нечётные цифры в числе должны чередоваться, составим схемы, на схемах красным цветом записана цифра 8 – это именно цифра в записи числа, но не количество вариантов цифр.
Для первой записи числа, на второй позиции может находится 5 различных вариантов цифр – любая из нечетных, на третьей – 4 варианта четных цифр – 0,2,4,6.
Для второй записи числа, на первой и третьей позициях может находится 5 различных вариантов цифр – любая из нечетных.
Для третьей записи числа, на первой позиции может находится 3 различных варианта цифр – 2,4,6, на второй – любая из 5 нечетных цифр.

Для каждой схему посчитаем количество комбинаций по правилу перемножения и затем сложим получившиеся результаты.
Количество трёхзначных чисел, записанных в десятичной системе счисления, в записи которых ровно одна цифра 8, при этом чётные и нечётные цифры чередуются, равно 60.
Ответ: 60
Задача №14
Определите количество пятизначных чисел, записанных в восьмеричной системе счисления, в записи которых нет цифры 0 и ровно две цифры 4, не стоящие рядом.
Решение
Восьмеричная система исчисления состоит из 8 цифр – 0, 1, 2, 3, 4, 5, 6, 7. При этом число не может начинаться на 0.
Найдем общее количество способов, которыми можно разместить две цифры 4 на пяти позициях:

Нам не подходят те способы, в которых цифры стоят рядом:

То есть нам подходят 10 – 4 = 6 способов.

На три оставшиеся позиции после размещения четверок можно поставить цифры 1, 2, 3, 5, 6, 7 – всего 6 вариантов:

Количество подходящих способов разместить четверки мы нашли, оно равно 6. Воспользуемся правилом перемножения для вычисления количества комбинаций – 6*6*6*6 = 1296.
Количество пятизначных чисел, записанных в восьмеричной системе счисления, в записи которых нет цифры 0 и ровно две цифры 4, не стоящие рядом, равно 1296.
Ответ: 1296
Задачи из демоверсии 2026 года по информатике с сайта ФИПИ.
Для решения подобных задач нужно запомнить принцип:
Пятибуквенные слова — это количество цифр в числе, то есть пятизначные числа.
Составленные из букв: С, Т, Р, О, К, А — это алфавит системы счисления, то есть какая система счисления будет использоваться.
Проведем сортировку по алфавиту, чтобы без ошибок расставить для каждой буквы соответствующую цифру.
А — 0
К — 1
О — 2
Р — 3
С — 4
Т — 5
В нашем случае: пятеричные числа в шестеричной системе счисления.
Напоминаю, так как нумерация начинается с 1, то к результату полученному нужно прибавить +1
Последнее слово с чётным номером — означает, что ищем максимальное пятизначное число в шестеричной системе счисления.
Не начинается с букв А, С или Т — в начале числа нет цифр 0, 4 или 5
При этом содержит в своей записи ровно две буквы О — это говорит нам о том, что необходимо расставить приоритетно буквы О, в зависимости от их числового значения.
Так как мы ищем максимально возможное число, то на первое место поставим Р — 3.
Р _ _ _ _
Так как буква О — 2 меньше, чем С — 4 и Т — 5, то О — 2 ставим в конце, а буквами Т — 5 заполним оставшееся место в числе.
Р _ _ О О
Р Т Т О О
Запишем в виде числа.
3 5 5 2 2
Это будет на максимальный вариант, но нужно проверить, будет ли номер числа чётным.
Номер 5163 нечётный, нам не подходит.
Пробуем вариант, который отличается нашего первого, но сохраняет соответствие условиям.
Кто уже догадался, что О — 2 в конце числа не может быть по причине того, что все равно в списке число будет нечетным из за того, что оно само по себе будет чётным + 1.
Значит расставляем буквы так, чтобы были две О — 2, но не последними цифрами.
Р Т О О Т
3 5 2 2 5
ответ: 5058

